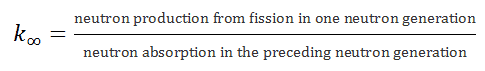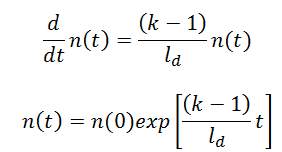The
infinite multiplication factor is the ratio of the
neutrons produced by fission in one
neutron generation to the number of
neutrons lost through absorption in the preceding neutron generation. The infinite multiplication factor (k
∞) may be expressed mathematically in terms of these factors by the following equation, usually known as the
four-factor formula:
k∞ = η.ε.p.f
In this section, the infinite multiplication factor, which describes all the possible events in the life of a neutron and effectively describes the state of an infinite multiplying system, will be defined.
The necessary condition for a stable, self-sustained fission chain reaction in a multiplying system (in a nuclear reactor) is that exactly every fission initiates another fission. The minimum condition is for each nucleus undergoing fission to produce, on average, at least one neutron that causes fission of another nucleus. Also, the number of fissions occurring per unit time (the reaction rate) within the system must be constant.
This condition can be expressed conveniently in terms of the multiplication factor. The infinite multiplication factor is the ratio of the neutrons produced by fission in one neutron generation to the number of neutrons lost through absorption in the preceding neutron generation. This can be expressed mathematically, as shown below.
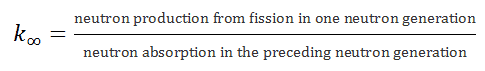
The infinite multiplication factor in a multiplying system measures the change in the fission neutron population from one neutron generation to the subsequent generation.
- k∞ < 1. Suppose the multiplication factor for a multiplying system is less than 1.0. In that case, the number of neutrons decreases in time (with the mean generation time), and the chain reaction will never be self-sustaining. This condition is known as the subcritical state.
- k∞ = 1. If the multiplication factor for a multiplying system is equal to 1.0, then there is no change in neutron population in time, and the chain reaction will be self-sustaining. This condition is known as the critical state.
- k∞ > 1. If the multiplication factor for a multiplying system is greater than 1.0, then the multiplying system produces more neutrons than are needed to be self-sustaining. The number of neutrons is exponentially increasing in time (with the mean generation time). This condition is known as the supercritical state.
From the multiplication factor to the reactor control
The simplest equation governing the neutron kinetics of the system with delayed neutrons is the point kinetics equation. This equation states that the time change of the neutron population is equal to the
excess of neutron production (by
fission)
minus neutron loss by absorption
in one mean generation time with delayed neutrons (ld). The role of
ld and
keff is evident. Larger
keff give a larger response and l
onger lifetimes give simply slower responses of multiplying systems.
If there are neutrons in the system at t=0, that is, if n(0) > 0, the solution of this equation gives the simplest point kinetics equation with delayed neutrons (similarly to the case without delayed neutrons):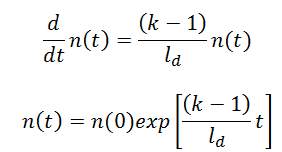
Let us consider that the mean generation time with delayed neutrons is ~0.085, and k (keff – neutron multiplication factor) will be increased by only 0.01% (i.e., 10pcm or ~1.5 cents), k∞=1.0000 will increase to k∞=1.0001.
It must be noted such reactivity insertion (10pcm) is very small in the case of LWRs. The reactivity insertions of the order of one pcm are for LWRs practically unrealizable. In this case, the reactor period will be:
T = ld / (k∞-1) = 0.085 / (1.0001-1) = 850s
This is a very long period. In ~14 minutes, the reactor’s neutron flux (and reactor power) would increase by a factor of e = 2.718. This is a completely different dimension of the response on reactivity insertion compared to the case without delayed neutrons, where the reactor period was 1 second.
Reactors with such kinetics would be quite easy to control. From this point of view, it may seem that reactor control will be quite a boring affair. It will not! The presence of delayed neutrons entails many specific phenomena that will be described in later chapters.
Four-Factor Formula
But the infinite multiplication factor can also be defined in terms of the most important neutron-physical processes in the nuclear reactor. For simplicity, we will first consider a multiplying system that is infinitely large and therefore has no neutron leakage. In the infinite system. Four-factors are completely independent of the size and shape of the reactor that describes the inherent multiplication ability of the fuel and moderator materials without regard to leakage:
Fast Fission Factor
The fast fission process is in the multiplication factor characterized by the fast fission factor, ε, which increases the fast neutron population in one neutron generation. The fast fission factor is the ratio of the fast neutrons produced by fissions at all energies to the number of fast neutrons produced in thermal fission.
Resonance Escape Probability
The resonance escape probability, symbolized by p, is the probability that a neutron will be slowed to thermal energy and will escape
resonance capture. This probability is defined as the ratio of the number of neutrons that reach thermal energies to the number of fast neutrons that slow down.
Thermal Utilization Factor
The thermal utilization factor, f, is the fraction of the
thermal neutrons that are absorbed in the
nuclear fuel, in all isotopes of the nuclear fuel. It describes how effectively (how well they are utilized) thermal neutrons are absorbed in the fuel. The value of the thermal utilization factor is given by the ratio of the number of thermal neutrons absorbed in the fuel (all nuclides) to the number of thermal neutrons absorbed in all the material that makes up the
core.
Reproduction Factor
The number of neutrons created in the new generation is determined by
the neutron reproduction factor.
The reproduction factor, η, is defined as the ratio of the number of fast neutrons produced by thermal fission to the number of
thermal neutrons absorbed in the fuel.
See also: Fast Fission Factor
See also: Resonance Escape Probability
See also: Thermal Utilization Factor
See also: Reproduction Factor
The infinite multiplication factor (k∞) may be expressed mathematically in terms of these factors by the following equation, usually known as the four-factor formula:
k∞ = η.ε.p.f
In reactor physics, k∞ or its finite form keff is the most significant parameter with regard to reactor control. At any specific power level or condition of the reactor, keff is kept as near to the value of 1.0 as possible. At this point in the operation, the neutron balance is kept to exactly one neutron completing the life cycle for each original neutron absorbed in the fuel.
From infinite to an effective multiplication factor
The infinite multiplication factor is derived based on the assumption that no neutrons leak out of the reactor (i.e., a reactor is infinitely large). But in reality, each nuclear reactor is finite, and neutrons can leak out of the reactor core. The multiplication factor that takes neutron leakage into account is the effective multiplication factor – keff, which is the ratio of the neutrons produced by fission in one neutron generation to the number of neutrons lost through absorption and leakage in the preceding neutron generation. The effective multiplication factor (keff) may be expressed mathematically in terms of the infinite multiplication factor (k∞) and two additional factors which account for neutron leakage during neutron thermalization (fast non-leakage probability) and neutron leakage during neutron diffusion (thermal non-leakage probability) by following equation, usually known as the six-factor formula:
keff = k∞ . Pf . Pt
Six Factor Formula - Fast Reactors
The method of calculations of multiplication factors has been developed
in the early years of nuclear energy and is only applicable to
thermal reactors, where the bulk of fission reactions occurs at thermal energies. This method puts into context all the processes associated with the thermal reactors (e.g.,, neutron thermalization, neutron diffusion, or fast fission) because the most important neutron-physical processes occur in energy
regions that can be clearly separated from each other. In short, the calculation of the multiplication factor gives a good insight into the processes that occur in each thermal multiplying system.
For fast reactors, in which the fission is caused by neutrons with a very broad energy distribution, such an analysis is inappropriate. The neutron flux in fast reactors has to be divided into many energy groups. Moreover, in fast reactors, neutron thermalization is an undesirable process, and therefore the four-factor formula does not make any sense. The resonance escape probability is insignificant because very few neutrons exist at energies where resonance absorption is significant. The thermal non-leakage probability does not exist because the reactor is designed to avoid the thermalization of neutrons.
Fast vs. Thermal Flux Spectrum
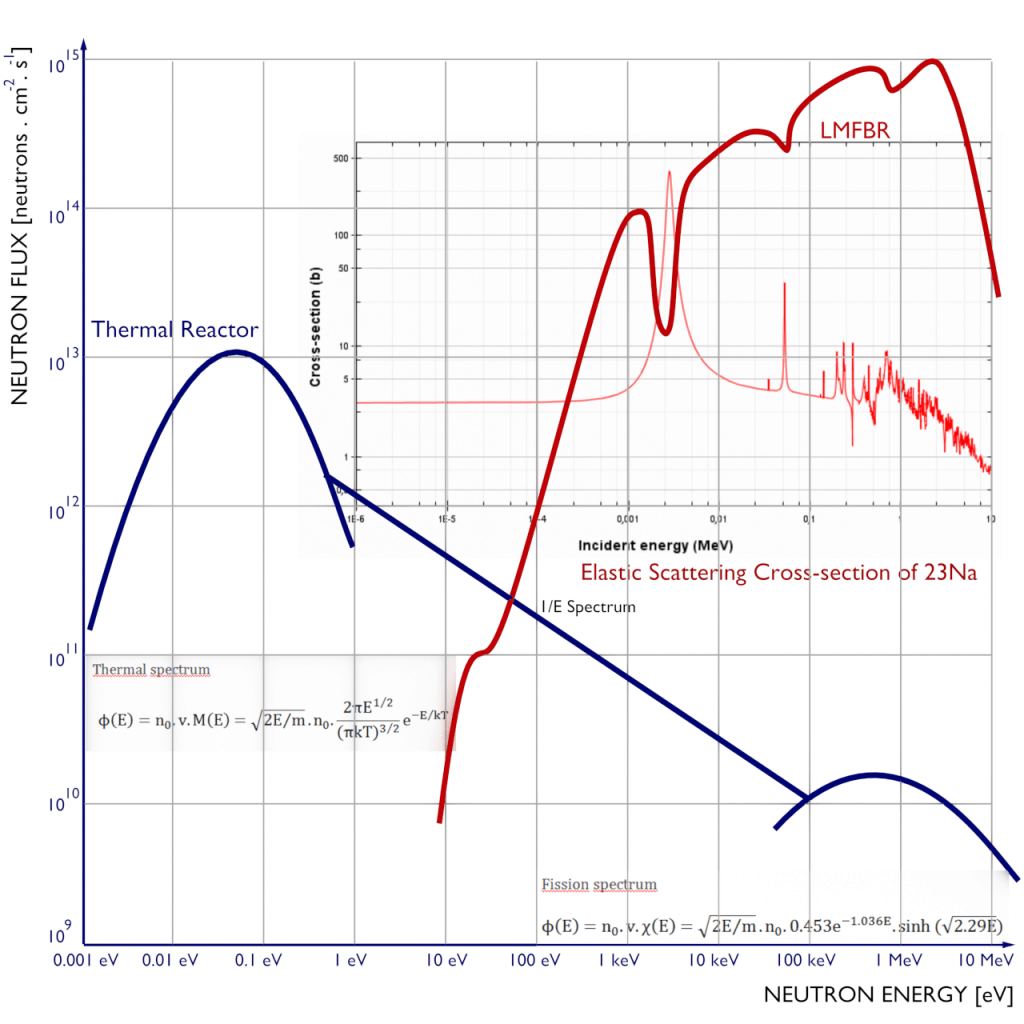
The spectrum of neutron energies produced by fission vary significantly with certain reactor design. thermal vs. fast reactor neutron spectrum
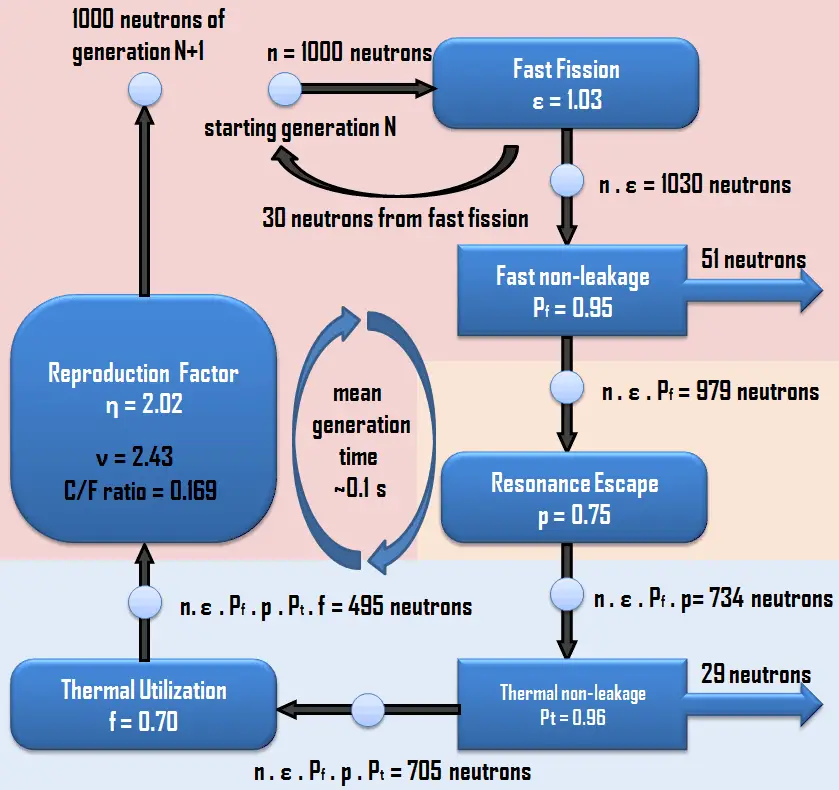
Operational factors that affect the multiplication in PWRs.
Detailed knowledge of all possible operational factors that may affect the multiplication factor of the system is of importance in reactor control. It was stated the keff is during reactor operation kept as near to the value of 1.0 as possible. Many factors influence the criticality of the reactor. For illustration, in an extreme case, the presence of humans (due to the water, carbon, which are good neutron moderators) near fresh uranium fuel assembly influences the multiplication properties of the assembly. If any operational factor changes one of the contributing factors to keff (keff = η.ε.p.f.Pf.Pt), the ratio of 1.0 is not maintained. This change in keff makes the reactor either subcritical or supercritical. Some examples of these operational changes in PWRs are below and are described in a separate article in detail.
- change in the control rods position
- change in the boron concentration
- change in the moderator temperature
- change in the fuel temperature
- change in the pressure
- change in the flow rate
- presence of boiling of the coolant
- presence of burnable absorbers
- fuel burnup
See also: Operational changes that affect the multiplication in PWRs.
References:
Nuclear and Reactor Physics:
- J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
- J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
- W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
- Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
- W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
- G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
- Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
- U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
Advanced Reactor Physics:
- K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
- K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
- D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
- E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.
See above:
Chain Reaction