Facebook Instagram Youtube Twitter

Neutron Generation – Neutron Population

In both terms, the neutron generation and the neutron population are closely associated with the multiplication of neutrons in the reactor core. The infinite multiplication factor is the ratio of the neutrons produced by fission in one neutron generation to the number of neutrons lost through absorption in the preceding neutron generation. This can be expressed mathematically, as shown below.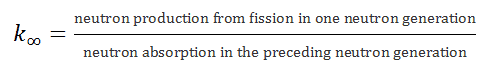Multiplication Factor

Example:

The following example may well express the difference:

Example:

The number of neutrons (the neutron population) in the core at time zero is 1000 and k∞ = 1.001 (~100 pcm).

Calculate the number of neutrons after 100 generations. Let say the mean generation time is ~0.1s.

Solution:
To calculate the neutron population after 100 neutron generations, we use following equation:

Nn=N0. (k∞)n
N1=N0.1.001 = 1001 neutrons after one generation
N2=N0.1.001.1.001 = 1002 neutrons after two generations
N3=N0.1.001.1.001.1.001 = 1003 neutrons after three generations
.
.

N50=N0. (k∞)50 = 1051 neutrons after fifty generations.

.

.

N100=N0. (k∞)100 = 1105 neutrons after hundred generations.

If we consider the mean generation time to be ~0.1s, the increase from 1000 neutrons to 1105 neutrons occurs within 10 seconds.

The infinite multiplication factor in a multiplying system measures the change in the fission neutron population from one neutron generation to the subsequent generation.

  • k∞ < 1. Suppose the multiplication factor for a multiplying system is less than 1.0. In that case, the number of neutrons decreases in time (with the mean generation time), and the chain reaction will never be self-sustaining. This condition is known as the subcritical state.
  • k∞ = 1. If the multiplication factor for a multiplying system is equal to 1.0, then there is no change in neutron population in time, and the chain reaction will be self-sustaining. This condition is known as the critical state.
  • k∞ > 1. If the multiplication factor for a multiplying system is greater than 1.0, then the multiplying system produces more neutrons than are needed to be self-sustaining. The number of neutrons is exponentially increasing in time (with the mean generation time). This condition is known as the supercritical state.
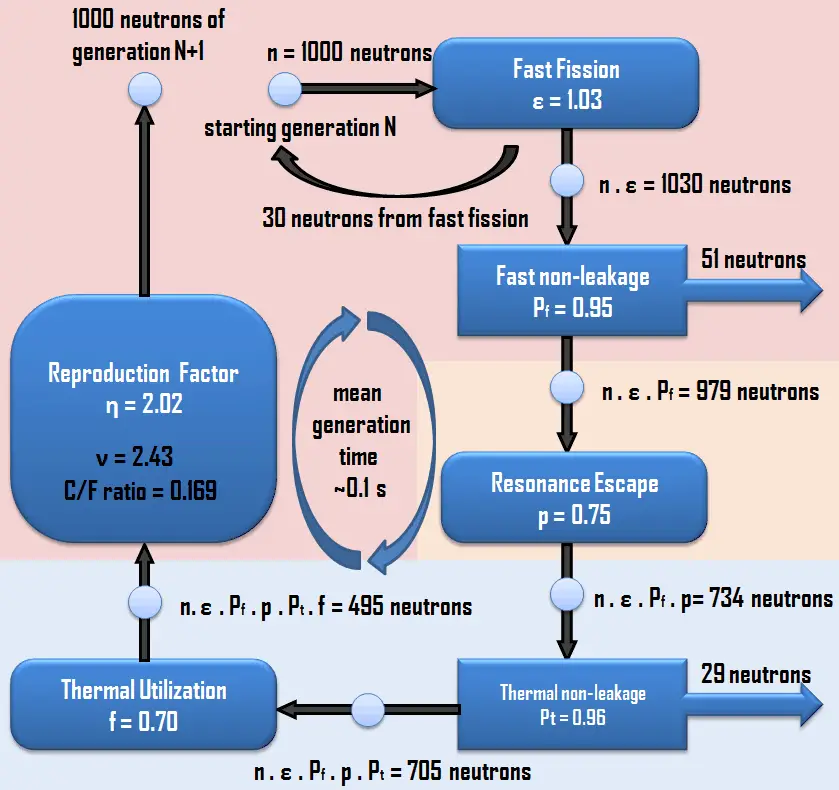
Nuclear Fission Chain Reaction
Neutron Life Cycle.
The sequence of fission events is known as the fission chain reaction, and it is important in nuclear reactor physics. The chain reaction can take place only in the proper multiplication environment and only under proper conditions.
 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2. 
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See previous:

See above:

Neutron Nuclear Reactions

See next: