Reactivity Coefficients

Reactivity feedbacks are inherent feedbacks that determine the stability of the reactor. Reactivity coefficients characterize these feedbacks. Reactivity coefficients are the amount that the reactivity will change for a given change in the parameter. Reactor design must assure that under all operating conditions, the temperature feedback will be negative.

According to 10 CFR Part 50; Criterion 11:

“The reactor core and associated coolant systems shall be designed so that in power operating range, the net effect of the prompt inherent nuclear feedback characteristics tends to compensate for a rapid increase in reactivity.

Up to this point, we have discussed the response of the neutron population in a nuclear reactor to an external reactivity input. There was applied an assumption that the level of the neutron population does not affect the properties of the system, especially that the neutron power (power generated by chain reaction) is sufficiently low that the reactor core does not change its temperature (i.e.,, reactivity feedbacks may be neglected). For this reason, such treatments are frequently referred to as zero-power kinetics.

However, in an operating power reactor, the neutron population is always large enough to generate heat. It is the main purpose of power reactors to generate a large amount of heat. This causes the system’s temperature to change and material densities to change as well (due to the thermal expansion).

Demonstration of the prompt negative temperature coefficient at the TRIGA reactor. A major factor in the prompt negative temperature coefficient for the TRIGA cores is the core spectrum hardening that occurs as the fuel temperature increases. This factor allows TRIGA reactors to operate safely during either steady-state or transient conditions.

Source: Youtube

Example: Change in the moderator temperature.

Negative feedback as the moderator temperature effect influences the neutron population in the following way. If the temperature of the moderator is increased, negative reactivity is added to the core. This negative reactivity causes reactor power to decrease. As the thermal power decreases, the power coefficient acts against this decrease, and the reactor returns to the critical condition. The reactor power stabilizes itself. In terms of multiplication factor, this effect is caused by significant changes in the resonance escape probability and total neutron leakage (or in the thermal utilization factor when the chemical shim is used).

Resonance escape probability

↑T_M ⇒ ↓k_eff = η.ε. ↓p . ↑f . ↓P_f. ↓P_t (BOC)

↑T_M ⇒ ↓k_eff = η.ε. ↓p .f. ↓P_f. ↓P_t (EOC)

Resonance escape probability. It is known, the resonance escape probability is also dependent on the moderator-to-fuel ratio. As the moderator temperature increases, the ratio of the moderating atoms (molecules of water) decreases due to the thermal expansion of water. Its density decreases. This, in turn, causes hardening of neutron spectrum in the reactor core resulting in higher resonance absorption (lower p). Decreasing the density of the moderator causes that neutrons stay at a higher energy for a longer period, which increases the probability of non-fission capture of these neutrons. This process is one of two processes (or three if the chemical shim is used) that determine the moderator temperature coefficient.

Thermal utilization factor

↑T_M ⇒ ↓k_eff = η.ε. ↓p . ↑f . ↓P_f. ↓P_t (BOC)

↑T_M ⇒ ↓k_eff = η.ε. ↓p .f. ↓P_f. ↓P_t (EOC)

Thermal utilization factor. The impact on the thermal utilization factor depends strongly on the amount of boron that is diluted in the primary coolant (chemical shim). As the moderator temperature increases, the density of water decreases due to the thermal expansion of water. But along with the moderator also boric acid is expanded out of the core. Since boric acid is a neutron poison, expanding out of the core, positive reactivity is added. The positive reactivity addition due to the expansion of boron out of the core offsets the negative reactivity addition due to the expansion of the moderator out of the core. Obviously, this effect is significant at the beginning of the cycle (BOC) and gradually loses its significance as the boron concentration decreases.

Neutron leakage

↑T_M ⇒ ↓k_eff = η.ε. ↓p . ↑f . ↓P_f. ↓P_t (BOC)

↑T_M ⇒ ↓k_eff = η.ε. ↓p .f. ↓P_f. ↓P_t (EOC)

Change of the neutron leakage. Since both (P_f and P_t) are affected by a change in moderator temperature in a heterogeneous water-moderated reactor and the directions of the feedbacks for both negative, the resulting total non-leakage probability is also sensitive to the change in the moderator temperature. As a result, an increase in the moderator temperature causes that the probability of leakage to increase. In the case of the fast neutron leakage, the moderator temperature influences macroscopic cross-sections for elastic scattering reaction (Σ_s=σ_s.N_H2O) due to the thermal expansion of water, which increases the moderation length. This, in turn, causes an increase in the leakage of fast neutrons.

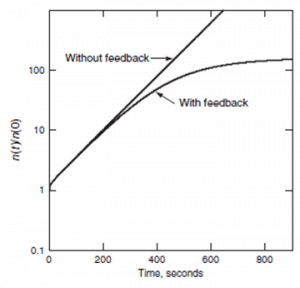
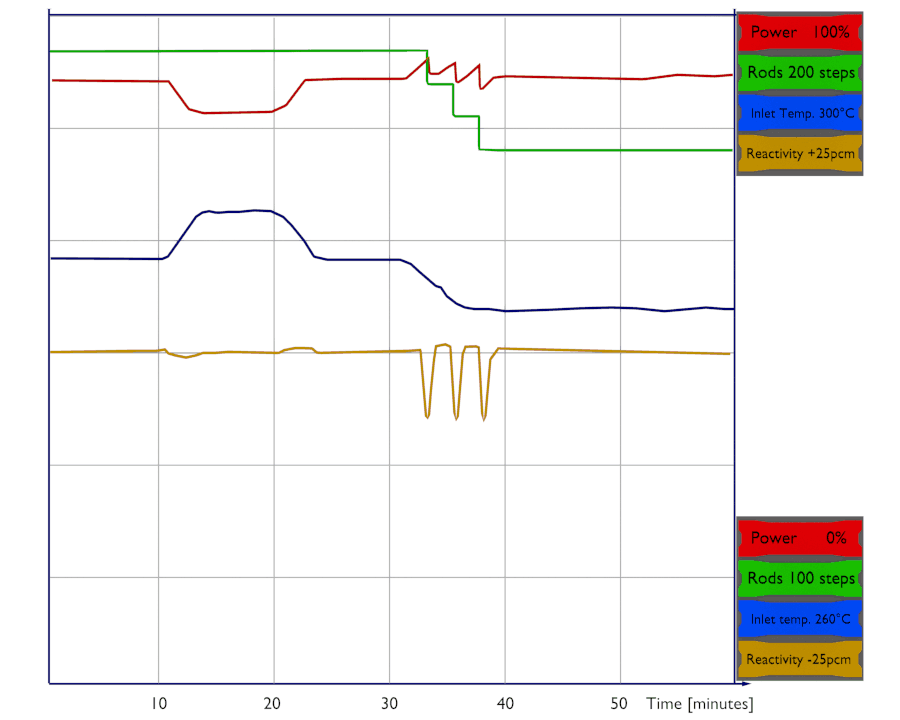
For the thermal neutron leakage, there are two effects. Both processes have the same direction and together cause the increase in the thermal neutron leakage. This physical process is a part of the moderator temperature coefficient (MTC).
- Macroscopic cross-sections for elastic scattering reaction Σ_s=σ_s.N_H2O, which significantly changes due to the thermal expansion of water. As the temperature of the core increases, the diffusion coefficient (D = 1/3.Σ_tr) increases.
- Microscopic cross-section (σ_a) for neutron absorption changes with core temperature. As the temperature of the core increases, the absorption cross-section decreases.

This figure shows the power excursion as a result of positive reactivity on a logarithmic scale. There is a curve without feedback and a curve for the same reactivity insertion but for which the effects of negative temperature feedback are included. It can be seen both curves initially follow the same, but as the power becomes larger, the curve with feedback becomes concave downward and stabilizes at constant power. At this point, the negative feedback has completely compensated for the initial reactivity insertion.

moderator temperature coefficient - MTC — Example: Increase in the core inlet temperature. If the temperature of the moderator is increased, negative reactivity is added to the core. This negative reactivity causes reactor power to decrease. As the thermal power decreases, the power coefficient acts against this decrease, and the reactor returns to the critical condition. The reactor power stabilizes itself. If the temperature of the moderator is decreased, the positive reactivity is offset by the control rod’s motion.

Examples: Change in the reactor power

Power increase – from 75% up to 100%

During any power increase, the temperature, pressure, or void fraction change and the reactivity of the core changes accordingly. It is difficult to
change an operating parameter and not affect every other property of the core. Since it is difficult to separate all these effects (moderator, fuel, void, etc.), the power coefficient is defined. The power coefficient combines the Doppler, moderator temperature, and void coefficients. It is expressed as a change in reactivity per change in percent power, Δρ/Δ% power. The value of the power coefficient is always negative in core life. Still, it is more negative at the end of the cycle primarily due to the decrease in the moderator temperature coefficient.

Let us assume that the reactor is critical at 75% of rated power and that the plant operator wants to increase power to 100% of rated power. The reactor operator must first bring the reactor supercritical by inserting a positive reactivity (e.g.,, by control rod withdrawal or boron dilution). As the thermal power increases, moderator temperature and fuel temperature increase, causing a negative reactivity effect (from the power coefficient), and the reactor returns to the critical condition. Positive reactivity must be continuously inserted (via control rods or chemical shim) to keep the power to be increasing. After each reactivity insertion, the reactor power stabilizes itself proportionately to the reactivity inserted. The total amount of feedback reactivity that must be offset by control rod withdrawal or boron dilution during the power increase (from ~1% – 100%) is known as the power defect.

Let assume:

the power coefficient: Δρ/Δ% = -20pcm/% of rated power
differential worth of control rods: Δρ/Δstep = 10pcm/step
worth of boric acid: -11pcm/ppm
desired trend of power decrease: 1% per minute

75% → ↑ 20 steps or ↓ 18 ppm of boric acid within 10 minutes → 85% → next ↑ 20 steps or ↓ 18 ppm within 10 minutes → 95% → final ↑ 10 steps or ↓ 9 ppm within 5 minutes → 100%

Power decrease – from 100% to 75%

During any power decrease, the temperature, pressure, or void fraction change and the reactivity of the core changes accordingly. It is difficult to change an operating parameter and not affect every other property of the core. Since it is difficult to separate all these effects (moderator, fuel, void, etc.), the power coefficient is defined. The power coefficient combines the Doppler, moderator temperature, and void coefficients. It is expressed as a change in reactivity per change in percent power, Δρ/Δ% power. The value of the power coefficient is always negative in core life. Still, it is more negative at the end of the cycle primarily due to the decrease in the moderator temperature coefficient.

Let us assume that the reactor is critical at 100% of rated power and that the plant operator wants to decrease power to 75% of rated power. The reactor operator must first bring the reactor subcritical by inserting a negative reactivity (e.g.,, by control rod insertion or boric acid addition). As the thermal power decreases, moderator temperature and fuel temperature decrease, causing a positive reactivity effect (from the power coefficient), and the reactor returns to the critical condition. Negative reactivity must be continuously inserted (via control rods or chemical shim) to keep the power decreasing. After each reactivity insertion, the reactor power stabilizes itself proportionately to the reactivity inserted.

Let assume:

the power coefficient: Δρ/Δ% = -20pcm/% of rated power
differential worth of control rods: Δρ/Δstep = 10pcm/step
worth of boric acid: -11pcm/ppm
desired trend of power decrease: 1% per minute

100% → ↓ 20 steps or ↑ 18 ppm of boric acid within 10 minutes → 90%→ next ↓ 20 steps or ↑ 18 ppm within 10 minutes → 80% → final ↓ 10 steps or ↑ 9 ppm within 5 minutes→ 75%

To describe the influence of all these processes on reactivity, one defines the reactivity coefficient α. A reactivity coefficient is defined as the change of reactivity per unit change in some operating parameter of the reactor. For example:

α = ^dρ⁄_dT

The amount of reactivity, which is inserted into a reactor core by a specific change in an operating parameter, is usually known as the reactivity effect and is defined as:

dρ = α . dT

The reactivity coefficients that are important in power reactors (PWRs) are:

As can be seen, there are not only temperature coefficients that are defined in reactor dynamics. In addition to these coefficients, there are two other coefficients:

The total power coefficient is the combination of various effects and is commonly used when reactors are at power conditions. It is because, at power conditions, it is difficult to separate the moderator effect from the fuel effect and the void effect. All these coefficients will be described in the following separate sections. The reactivity coefficients are of importance in the safety of each nuclear power plant which is declared in the Safety Analysis Report (SAR).

References:

Nuclear and Reactor Physics:

J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See above:

Reactor Criticality