The moderator temperature coefficient – MTC is defined as the change in reactivity per degree change in moderator temperature.
αM = dρ⁄dTM
It is expressed in units of pcm/°C or pcm/°F. The value of moderator temperature coefficient usually ranges from 0 pcm/°C to -80 pcm/°C. The moderator temperature coefficient’s magnitude and sign (+ or -) is primarily a function of the moderator-to-fuel ratio. That means it primarily depends on a specific reactor design. It must be noted, according to the design requirements (e.g.,, NUREG-0800, Chapter 4), reactor design must assure that:
“The MTC should be non-positive over the entire fuel cycle when the reactor is at a significant power level.”
Therefore all light water reactors (LWR) must be designed under moderated because it ensures that the reactor may have a negative moderator temperature coefficient. If a reactor is over moderated, it can not reach a positive moderator temperature coefficient. A negative moderator temperature coefficient is desirable because of its self-regulating effect.
The total amount of reactivity, which is inserted to a reactor core by a specific change in the moderator temperature, is usually known as the moderator reactivity defect and is defined as:
dρ = α . dT
Theory of Moderator Temperature Coefficient
It is very difficult to describe the physics of the moderator temperature coefficient because changes in moderator temperature lead to the change of almost all the parameters in a reactor core. For better understanding, we describe major physical mechanisms that occur in the moderator temperature coefficient in terms of the six-factor formula.
↑TM ⇒ ↓keff = η.ε. ↓p . ↑f . ↓Pf . ↓Pt (BOC)
↑TM ⇒ ↓keff = η.ε. ↓p .f. ↓Pf . ↓Pt (EOC)
Major impacts on the multiplication of the system arise from the change of the resonance escape probability and the change of total neutron leakage (see thermal non-leakage probability and fast non-leakage probability). But as can be seen at the beginning of the cycle (BOC), when the PWR core contains a large amount of boron dissolved in the primary coolant (chemical shim), an increase in temperature causes an increase in the thermal utilization factor.
 Change of the resonance escape probability. It is known, the resonance escape probability is also dependent on the moderator-to-fuel ratio. All PWRs are designed as under moderated reactors. As the moderator temperature increases, the ratio of the moderating atoms (molecules of water) decreases due to the thermal expansion of water. Its density simply decreases. This, in turn, causes hardening of neutron spectrum in the reactor core resulting in higher resonance absorption (lower p). The decreasing density of the moderator causes that neutrons stay at a higher energy for a longer period, which increases the probability of non-fission capture of these neutrons. It must be added moderator density changes are not linear. At high temperatures, an increase in the moderator temperature causes a larger reduction in density than an identical increase at low moderator temperatures. This process (the hardening of the neutron spectrum) is one of two key processes that determine the moderator temperature coefficient (MTC). The second process is connected with the leakage probability of the neutrons.
Change of the resonance escape probability. It is known, the resonance escape probability is also dependent on the moderator-to-fuel ratio. All PWRs are designed as under moderated reactors. As the moderator temperature increases, the ratio of the moderating atoms (molecules of water) decreases due to the thermal expansion of water. Its density simply decreases. This, in turn, causes hardening of neutron spectrum in the reactor core resulting in higher resonance absorption (lower p). The decreasing density of the moderator causes that neutrons stay at a higher energy for a longer period, which increases the probability of non-fission capture of these neutrons. It must be added moderator density changes are not linear. At high temperatures, an increase in the moderator temperature causes a larger reduction in density than an identical increase at low moderator temperatures. This process (the hardening of the neutron spectrum) is one of two key processes that determine the moderator temperature coefficient (MTC). The second process is connected with the leakage probability of the neutrons.
- Change of the neutron leakage. Since both (Pf and Pt) are affected by a change in moderator temperature in a heterogeneous water-moderated reactor and the directions of the feedbacks are the same, the resulting total non-leakage probability is also sensitive to the change in the moderator temperature. As a result, an increase in the moderator temperature causes that the probability of leakage to increase. In the case of the fast neutron leakage, the moderator temperature influences macroscopic cross-sections for elastic scattering reaction (Σs=σs.NH2O) due to the thermal expansion of water, which increases the moderation length. This, in turn, causes an increase in the leakage of fast neutrons.
- For the thermal neutron leakage, there are two effects. Both processes have the same direction and together cause the increase in the thermal neutron leakage. This physical process is a part of the moderator temperature coefficient (MTC).
- Macroscopic cross-sections for elastic scattering reaction Σs=σs.NH2O, which significantly changes due to the thermal expansion of water. As the temperature of the core increases, the diffusion coefficient (D = 1/3.Σtr) increases.
- Microscopic cross-section (σa) for neutron absorption changes with core temperature. As the temperature of the core increases, the absorption cross-section decreases.
- For the thermal neutron leakage, there are two effects. Both processes have the same direction and together cause the increase in the thermal neutron leakage. This physical process is a part of the moderator temperature coefficient (MTC).
- Change of the thermal utilization factor. The impact on the thermal utilization factor depends strongly on the amount of boron that is diluted in the primary coolant (chemical shim). As the moderator temperature increases, the density of water decreases due to the thermal expansion of water. But along with the moderator also boric acid is expanded out of the core. Since boric acid is a neutron poison, expanding out of the core, positive reactivity is added. The positive reactivity addition due to the expansion of boron out of the core offsets the negative reactivity addition due to the expansion of the moderator out of the core. The resulting MTC is therefore strongly dependent on the concentration of boron in the primary coolant. This effect is significant at the beginning of the cycle (BOC) and gradually loses significance as the boron concentration decreases. In the case of PWRs, burnable poisons are usually used to reduce the amount of dissolved boron. Without burnable absorbers, it would be impossible to reach non-positive MTC, especially today, when utilities demand vendors to design cores that can operate from 18 to 24 months at full power. In PWRs, samarium concentration can also influence the MTC at BOC. Note that the samarium peak concentration after shutdown is flux-dependent! The sudden shutdown of a reactor at the end of the cycle lowers MTC (lowers critical boron concentration) at the beginning of the next cycle.
Moderator Temperature Coefficient and Reactor Design
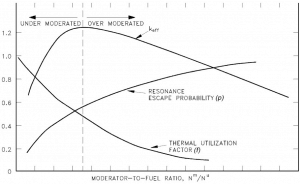
 As was written, the moderator temperature coefficient is primarily a function of the moderator-to-fuel ratio (NH2O/NFuel ratio). The moderator-to-fuel ratio is the ratio of the number of moderator nuclei within the reactor core volume to the number of fuel nuclei. As the core temperature increases, fuel volume and number density remain essentially constant. The volume of moderator also remains constant, but the number density of moderator decreases with thermal expansion. As the moderator temperature increases, the ratio of the moderating atoms (molecules of water) decreases due to the thermal expansion of water (especially at 300°C; see: Density of Water). Its density simply and significantly decreases. This, in turn, causes hardening of neutron spectrum in the reactor core resulting in higher resonance absorption (lower p). The decreasing density of the moderator causes that neutrons stay at a higher energy for a longer period, which increases the probability of non-fission capture of these neutrons. This process is one of three processes, which determine the moderator temperature coefficient (MTC). The second process is associated with the leakage probability of the neutrons and the third with the thermal utilization factor.
As was written, the moderator temperature coefficient is primarily a function of the moderator-to-fuel ratio (NH2O/NFuel ratio). The moderator-to-fuel ratio is the ratio of the number of moderator nuclei within the reactor core volume to the number of fuel nuclei. As the core temperature increases, fuel volume and number density remain essentially constant. The volume of moderator also remains constant, but the number density of moderator decreases with thermal expansion. As the moderator temperature increases, the ratio of the moderating atoms (molecules of water) decreases due to the thermal expansion of water (especially at 300°C; see: Density of Water). Its density simply and significantly decreases. This, in turn, causes hardening of neutron spectrum in the reactor core resulting in higher resonance absorption (lower p). The decreasing density of the moderator causes that neutrons stay at a higher energy for a longer period, which increases the probability of non-fission capture of these neutrons. This process is one of three processes, which determine the moderator temperature coefficient (MTC). The second process is associated with the leakage probability of the neutrons and the third with the thermal utilization factor.
The moderator-to-fuel ratio strongly influences especially:
- Resonance escape probability. An increase in the moderator-to-fuel ratio causes an increase in resonance escape probability. As more moderator molecules are added relative to the number of fuel molecules, then it becomes easy for neutrons to slow down to thermal energies without encountering a resonance absorption at the resonance energies.
- Thermal utilization factor. An increase in the moderator-to-fuel ratio causes a decrease in the thermal utilization factor. The value of the thermal utilization factor is given by the ratio of the number of thermal neutrons absorbed in the fuel (all nuclides) to the number of thermal neutrons absorbed in all the material that makes up the core.
- Thermal and fast non-leakage probability. An increase in moderator-to-fuel ratio causes a decrease in migration length, which in turn causes an increase in non-leakage probability.
As can be seen from the figure, at low moderator-to-fuel ratios, the product of all the six factors (keff) is small because the resonance escape probability is small. At an optimal value of the moderator-to-fuel ratio, keff reaches its maximum value. This is the case of so-called “optimal moderation”. At large ratios, keff is again small because the thermal utilization factor is small.
Under-moderated vs. Over-moderated Reactor
From the moderator-to-fuel ratio point of view, any multiplying system can be designed as:
- Under-moderated. Under-moderation means that there is less than the optimum amount of moderator between fuel plates or fuel rods. An increase in moderator temperature and voids decreases the keff of the system and inserts negative reactivity. An under-moderated core would create a negative temperature and void feedback required for a stable system.
- Over-moderated. Over-moderation means that there is a higher than optimum amount of moderator between fuel plates or fuel rods. An increase in moderator temperature and voids increases the keff of the system and inserts positive reactivity. An over-moderated core would create a positive temperature and void feedback. It will result in an unstable system unless another negative feedback mechanism (e.g.,, the Doppler broadening) overrides the positive effect.
Reactor engineers must balance the composite effects of moderator density, fuel temperature, and other phenomena to ensure system stability under all operating conditions. Most light water reactors are therefore designed as so-called under-moderated, and the neutron flux spectrum is slightly harder (the moderation is slightly insufficient) than in an optimum case. But this design provides an important safety feature. An increase in the moderator temperature results in negative reactivity, which tends to make the reactor self-regulating. It must be added, the overall feedback must be negative, but local positive coefficients exist in areas with large water gaps that are over-moderated such as near control rods guide tubes.
Another phenomenon associated with an under-moderated core is called the neutron flux trap effect. This effect causes an increase in local power generation due to better thermalization of neutrons in areas with large water gaps (between fuel assemblies or when the fuel assembly bow phenomenon is present). Note that “flux traps” are a standard feature of most modern test reactors because of the desire to obtain high thermal neutron fluxes for the irradiation of materials. Still, it can also occur in PWRs.
On the other hand, also under-moderation has its limits. In general, it causes a decrease in overall keff. Therefore more fissile material is needed to ensure criticality of the core. Moreover, there is also a limit on the minimal value of MTC (most negative). It is because the negative temperature feedback also acts against the decrease in the moderator temperature. Consider what happens when moderator temperature is decreased quickly, as in the case of the main steamline break (MSLB – standard initiating event for PWRs). The steamline break causes the steam pressure, the saturation temperature in the steam generators to fall rapidly. As a result of the falling saturation temperature in the steam generators, the moderator temperature will rapidly decrease. The rapid moderator temperature drop causes a positive reactivity insertion. The amount of reactivity inserted also depends on the magnitude of the MTC, and therefore it must be limited. The typical values for the lower limit are MTC = -80 pcm/°C, but it is a plant-specific value limited in technical specifications.