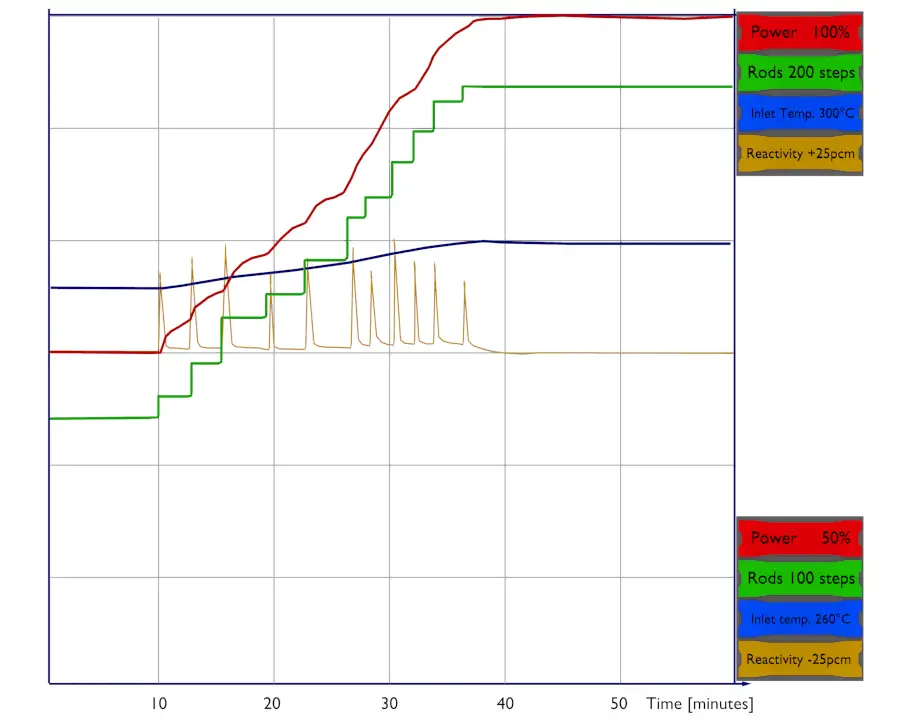
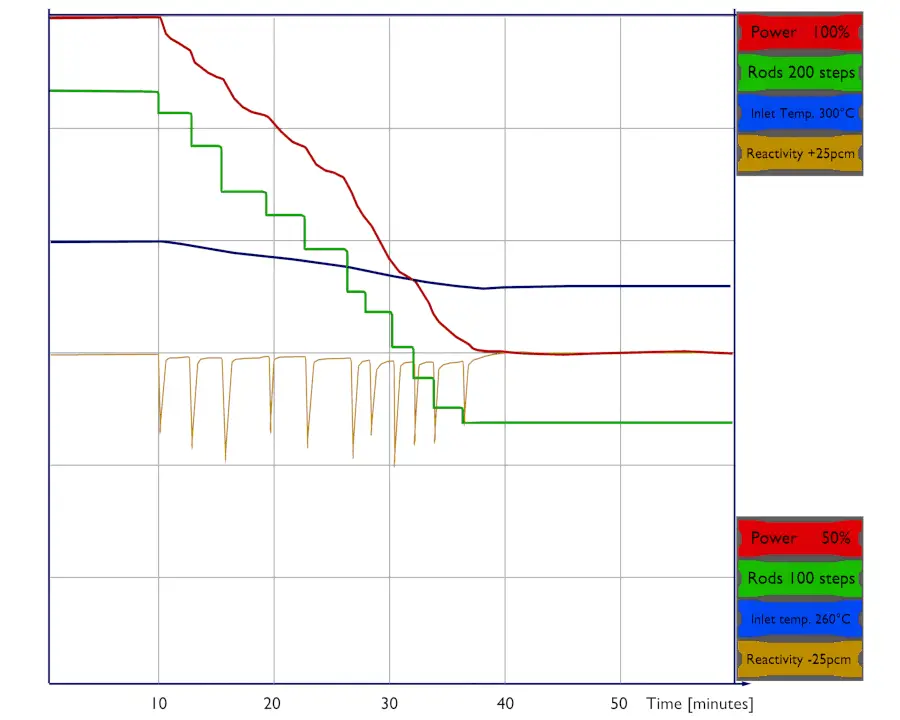
The total power coefficient – TPC is defined as the change in reactivity per percent change in the reactor power.
αP = Δρ/Δ% power
It is expressed in units of pcm/% power. It is defined for all states in which the reactor power changes. The power coefficient combines all the Doppler, moderator temperature, and void coefficients and is commonly used when reactors are at power operation (mode 1). It is because, at power conditions, it is difficult to separate (when the reactor power changes) the moderator effect from the fuel effect and the void effect as well.
In PWRs, the total power coefficient can range, for example, from -20 pcm/% to -30 pcm/%. The value of the power coefficient is always negative in core life. Still, it is more negative at the end of the cycle primarily due to the decrease in the moderator temperature coefficient.
It was written the total power coefficients combined all the Doppler, moderator temperature, and void coefficients. It is obvious, and it is a significant difference in power coefficients of PWRs and BWRs. The main difference is in the void effect. In the following points, the effects and their contribution to the power coefficient of PWRs will be discussed:
- Doppler effect. About 78% of power coefficient. In PWRs, the Doppler coefficient can range, for example, from -5 pcm/°C to -2 pcm/°C. It seems to be a small value, but it is a fact the power changes cause significant changes in the fuel temperature. The changes in the fuel temperature may be of the order of hundreds of °C. It must be added the doppler coefficient is also called the prompt temperature coefficient because it causes an immediate response to changes in fuel temperature. It is of the highest importance in reactor stability.
- Moderator temperature effect. About 20% of power coefficient. The value of the moderator temperature coefficient usually ranges from 0 pcm/°C to -80 pcm/°C (depending on the boron concentration).
- Void effect. About 2% of power coefficient. In pressurized water reactors, the void content of the core may be about one-half of one percent. Therefore this effect is marginal for the power coefficient in PWRs.
Let assume:
- the power coefficient: Δρ/Δ% = -20pcm/% of rated power
- differential worth of control rods: Δρ/Δstep = 10pcm/step
- worth of boric acid: -11pcm/ppm
- desired trend of power decrease: 1% per minute
75% → ↑ 20 steps or ↓ 18 ppm of boric acid within 10 minutes → 85% → next ↑ 20 steps or ↓ 18 ppm within 10 minutes → 95% → final ↑ 10 steps or ↓ 9 ppm within 5 minutes → 100%
Let assume:
- the power coefficient: Δρ/Δ% = -20pcm/% of rated power
- differential worth of control rods: Δρ/Δstep = 10pcm/step
- worth of boric acid: -11pcm/ppm
- desired trend of power decrease: 1% per minute
100% → ↓ 20 steps or ↑ 18 ppm of boric acid within 10 minutes → 90%→ next ↓ 20 steps or ↑ 18 ppm within 10 minutes → 80% → final ↓ 10 steps or ↑ 9 ppm within 5 minutes→ 75%
Power Defect
For power reactors at power conditions the reactor can behave differently as a result of the presence of reactivity feedbacks. Power reactors are initially started from hot standby mode (a subcritical state at 0% of rated power) to power operation mode (100% of rated power) by withdrawing control rods and boron dilution from the primary source coolant. During the reactor startup and up to about 1% of rated power, the reactor kinetics is exponential as in a zero-power reactor. This is due to the fact all temperature reactivity effects are minimal.
On the other hand, the temperature reactivity effects play a very important role during further power increase from about 1% up to 100% of rated power. As the neutron population increases, the fuel and the moderator increase their temperature, which results in a decrease in reactivity of the reactor (almost all reactors are designed to have the temperature coefficients negative).
The negative reactivity coefficient acts against the initial positive reactivity insertion and this positive reactivity is offset by negative reactivity from temperature feedbacks. Positive reactivity must be continuously inserted (via control rods or chemical shim) to keep the power to be increasing. After each reactivity insertion, the reactor power stabilizes itself on the power level proportionately to the reactivity inserted. The total amount of feedback reactivity that must be offset by control rod withdrawal or boron dilution during the power increase is known as the power defect. The power defects for PWRs, graphite-moderated reactors and sodium-cooled fast reactors are:
- about 2500pcm for PWRs,
- about 800pcm for graphite-moderated reactors
- about 500pcm for sodium-cooled fast reactors
The power defects slightly depend on the fuel burnup because they are determined by the power coefficient, which depends on the fuel burnup. The power coefficient combines the Doppler, moderator temperature, and void coefficients. The value of the power coefficient is always negative in core life. Still, it is more negative at the end of the cycle primarily due to the decrease in the moderator temperature coefficient.
It is logical, as the power coefficient acts against power increase, it also acts against power decrease. When reactor power is decreased quickly, as in the reactor trip, the power coefficient causes a positive reactivity insertion (as a result of the fuel temperature and the moderator temperature decrease), and the initial rod insertion must be sufficient to make the reactor safe subcritical.
It is obvious, if the power defect for PWRs is about 2500pcm (about 6 βeff), the control rods must weigh more than 2500pcm to achieve the subcritical condition. To ensure the safe subcritical condition, the control rods must weigh more than 2500pcm plus value of SDM (SHUTDOWN MARGIN). The total weigh of control rods is design specific, but, for example, it may reach about 6000pcm. To ensure that the control rods can safe shut down the reactor, they must be maintained above a minimum rod height (rods insertion limits) specified in the technical specifications.
