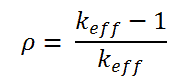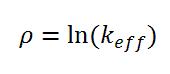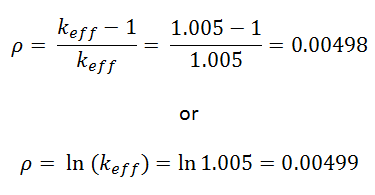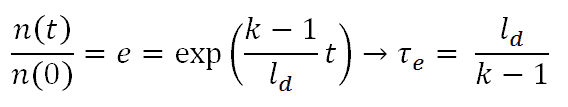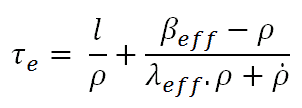Mathematically, reactivity is a dimensionless number, but various units can express it. The most common units for power reactors are units of pcm or %ΔK/K. For reactor core with βeff = 0.006 (0.6%), one dollar is equal to about 600 pcm. It is a very substantial amount of reactivity because if the core’s reactivity is one dollar, the reactor is prompt critical.
In the preceding chapters, the classification of states of a reactor according to the effective multiplication factor – keff was introduced. The effective multiplication factor – keff is a measure of the change in the fission neutron population from one neutron generation to the subsequent generation. But sometimes, it is convenient to define the change in the keff alone, the change in the state, from the criticality point of view.
For these purposes, reactor physics uses a term called reactivity rather than keff to describe the change in the state of the reactor core. The reactivity (ρ or ΔK/K) is defined in terms of keff by the following equation:
From this equation, it may be seen that ρ may be positive, zero, or negative. The reactivity describes the deviation of an effective multiplication factor from unity. For critical conditions, the reactivity is equal to zero. The larger the absolute reactivity value in the reactor core, the further the reactor is from criticality. The reactivity may be used as a measure of a reactor’s relative departure from criticality.
It must be noted the reactivity can also be calculated according to another formula.
This formula is widely used in neutron diffusion or neutron transport codes. The advantage of this reactivity is obvious, it is a measure of a reactor’s relative departure not only from criticality (keff = 1), but it can be related to any sub or supercritical state (ln(k2 / k1)). Another important feature arises from the mathematical properties of the logarithm. The logarithm of the division of k2 and k1 is the difference between the logarithm of k2 and the logarithm of k1. ln(k2 / k1) = ln(k2) – ln(k1). This feature is important in the case of addition and subtraction of various reactivity changes.
See more: D.E.Cullen, Ch.J.Clouse, R.Procassini, R.C.Little. Static and Dynamic Criticality: Are They Different?. Lawrence Livermore National Laboratory. UCRL-TR-201506. 11/2003.
The following formulas give the reactivity.
Units of Reactivity
Mathematically, reactivity is a dimensionless number, but various units can express it. The most common units for research reactors are units normalized to the delayed neutron fraction (e.g.,, cents and dollars) because they exactly express a departure from prompt criticality conditions.
The most common units for power reactors are units of pcm or %ΔK/K. The reason is simple. Units of dollars are difficult to use because the normalization factor, the effectively delayed neutron fraction, significantly changes with the fuel burnup. In LWRs, the delayed neutron fraction decreases with fuel burnup (e.g.,, from βeff = 0.007 at the beginning of the cycle up to βeff = 0.005 at the end of the cycle). This is due to isotopic changes in the fuel. It is simple. Fresh uranium fuel contains only 235U as the fissile material. Meanwhile, during fuel burnup, the importance of fission of 239Pu increases (in some cases up to 50%). Since 239Pu produces significantly fewer delayed neutrons (0.0021 for thermal fission), the resultant core delayed neutron fraction of a multiplying system decreases (it is the weighted average of the constituent delayed neutron fractions).
βcore= ∑ Pi.βi
dollar ($)
The unit of reactivity has been normalized to the delayed neutron fraction. Reactivity in dollars = ρ / βeff. The cent is 1/100 of a dollar. This is a very useful unit because the reactivity in dollars (rather in cents) determines exactly the response of the reactor on the reactivity insertion. Conversion of dollars to pcm depends on βeff. For reactor core with βeff = 0.006 (0.6%) one dollar is equal to about 600 pcm. It is a very substantial amount of reactivity because if the core’s reactivity is one dollar, the reactor is prompt critical.
BOC and βeff = 0.006
keff = 0.99 ρ = (keff – 1) / keff = -0.01 ρ = -0.01 / 0.006 = -1.67 $ = -167 cents
EOC and βeff = 0.005
keff = 0.99 ρ = (keff – 1) / keff = -0.01 ρ = -0.01 / 0.005 = -2.00 $ = -200 cents
%ΔK/K
The unit of reactivity in percent of the effective multiplication factor. For example, the subcriticality of keff = 0,98 equals -2% in units of %ΔK/K. Since this is a very large amount of reactivity, these units are usually used to express significant quantities of reactivity like power defects, xenon worth, the integral worth of control rods, or shutdown margin. This unit is inappropriate for operational changes that affect the effective multiplication factor because these changes are of the lower order.
keff = 0.99 ρ = (keff – 1) / keff = -0.01 ρ = -0.01 * 100% = -1 %
percent mille (pcm)
The reactivity unit is one-thousandth of a percent %ΔK/K (equal to 10-2x10-3 = 10-5 of keff). The unit of pcm is used at many LWRs because reactivity insertion values are generally quite small, and units of pcm allow reactivity to be written in whole numbers. The operational changes such as control rods movement usually cause reactivity insertion of the order of units of pcm per one step. The fact that the effective delayed neutron fraction changes with the fuel burnup have an important consequence. Due to the difference in βeff a response of a reactor on the same reactivity insertion (in units of pcm) is different at the beginning (BOC) and the end (EOC) of the cycle.
For example, one step of control rods causes a greater response at EOC than at BOC. Even though we assume that one step causes the same reactivity insertion (e.g.,, +10pcm) in both cases. Moreover, this assumption is not always correct because the control rod’s worth increases with fuel burnup.
(10 pcm = 1.43 cents for βeff = 0.007; 10 pcm = 2.00 cents for βeff = 0.005)
keff = 0.99 ρ = (keff – 1) / keff = -0.01 ρ = -0.01 * 105 = -1000 pcm
Reactivity in Reactor Kinetics
In the preceding chapters, the classification of states of a reactor according to the effective multiplication factor – keff was introduced. The effective multiplication factor – keff is a measure of the change in the fission neutron population from one neutron generation to the subsequent generation. Also, reactivity as a measure of a reactor’s relative departure from criticality was defined.
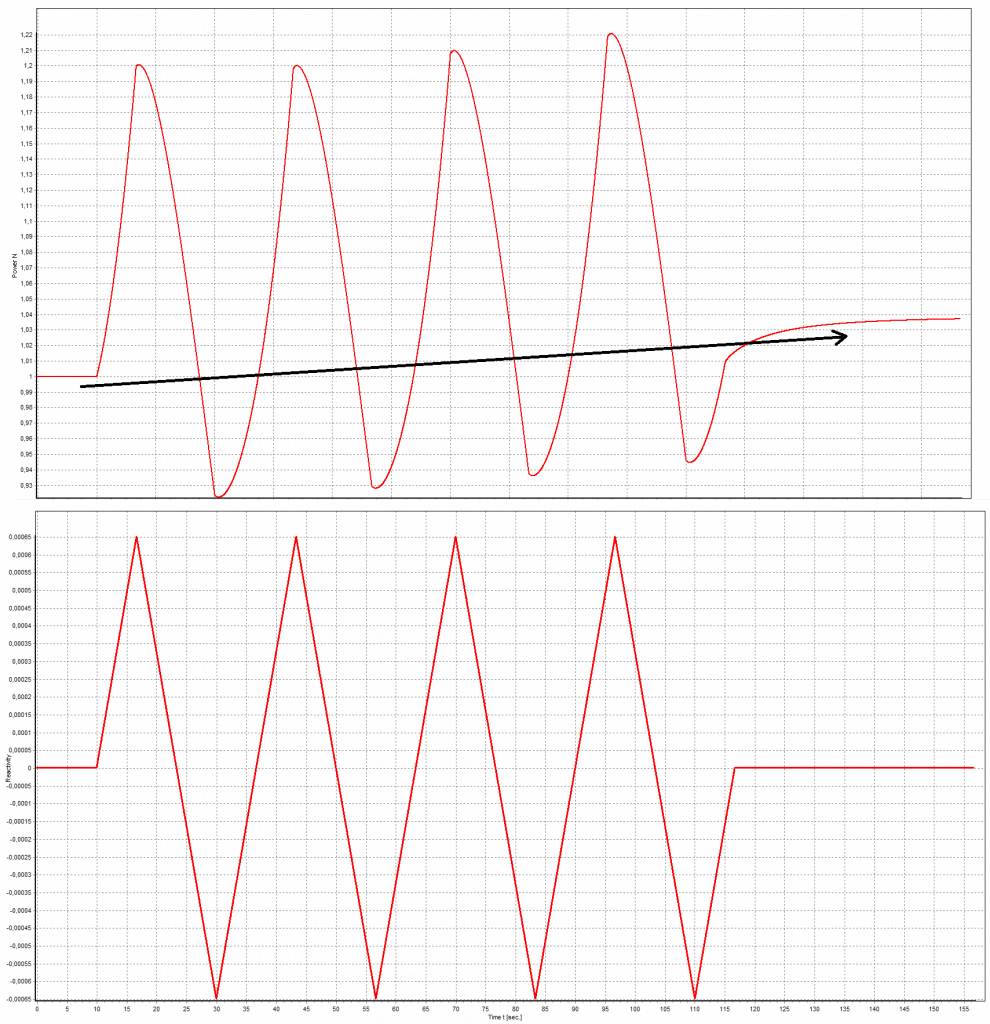
This section, amongst other things it will be briefly described how the neutron flux (i.e., the reactor power) changes if the reactivity of a multiplying system is not equal to zero. Understanding the time-dependent behavior of the neutron population in a nuclear reactor in response to either a planned change in the reactor’s reactivity or to unplanned and abnormal conditions is the most important in nuclear reactor safety. This subject is usually called reactor kinetics (without reactivity feedback) or reactor dynamics (with reactivity feedback and spatial effects).
Nuclear reactor kinetics deals with transient neutron flux changes resulting from a departure from the critical state, from some reactivity insertion. Such situations arise during operational changes such as control rods motion, environmental changes such as a change in boron concentration, or accidental disturbances in the reactor steady-state operation.
Point Kinetics Equation – One Delayed Neutron Group Approximation
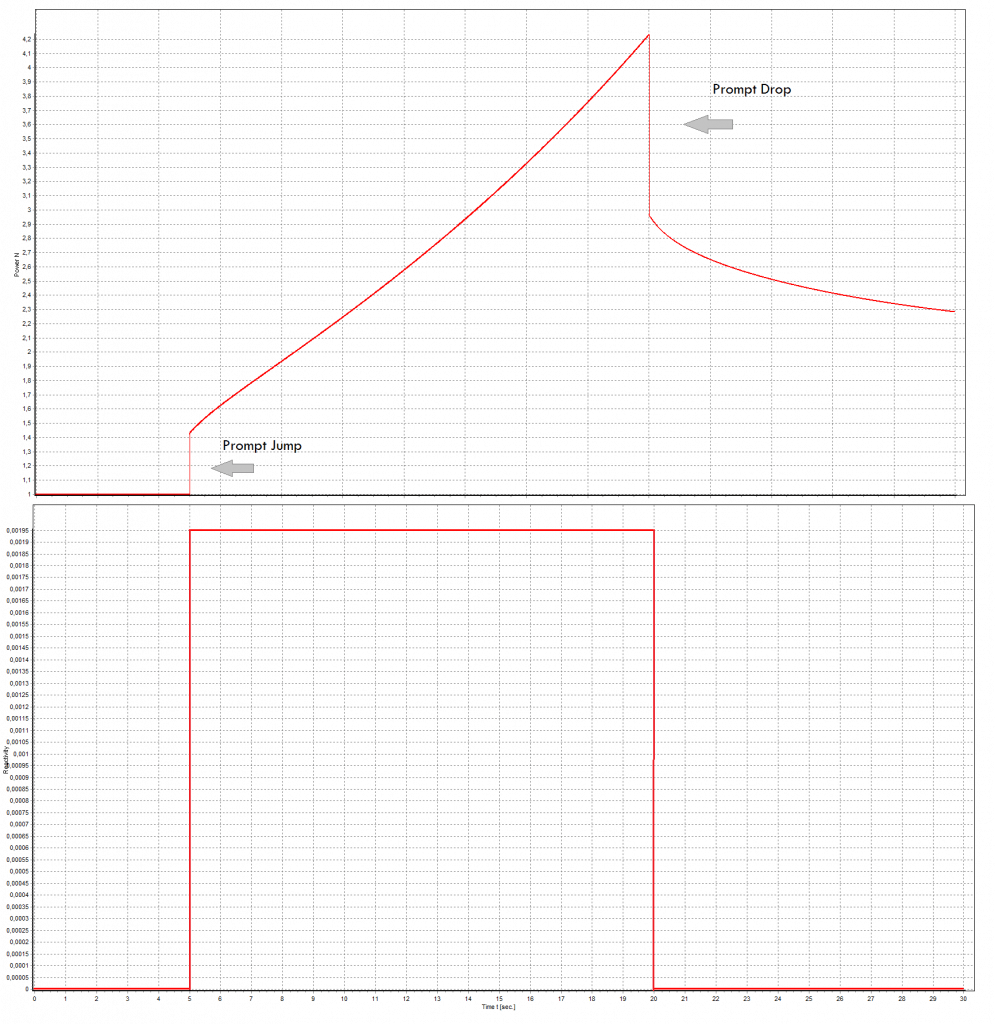
The simplest equation governing the neutron kinetics of the system with delayed neutrons is the point kinetics equation. This equation states that the time change of the neutron population is equal to the excess of neutron production (by fission) minus neutron loss by absorption in one mean generation time with delayed neutrons (ld). The role of ld is evident. Longer lifetimes give simply slower responses to multiplying systems. The role of reactivity (keff – 1) is also evident. Higher reactivity gives a simply larger response to the multiplying system.
If there are neutrons in the system at t=0, that is, if n(0) > 0, the solution of this equation gives the simplest point kinetics equation with delayed neutrons (similarly to the case without delayed neutrons):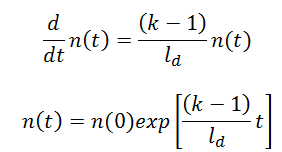
Let us consider that the mean generation time with delayed neutrons is ~0.085 and k (k∞ – neutron multiplication factor) will be step increased by only 0.01% (i.e., 10pcm or ~1.5 cents), that is k∞=1.0000 will increase to k∞=1.0001.
It must be noted such reactivity insertion (10pcm) is very small in the case of LWRs (e.g.,, one step by control rods). The reactivity insertions of the order of one pcm are for LWRs practically unrealizable. In this case, the reactor period will be:
T = ld / (k∞-1) = 0.085 / (1.0001-1) = 850s
This is a very long period. In ~14 minutes, the reactor’s neutron flux (and power) would increase by a factor of e = 2.718. This is a completely different dimension of the response on reactivity insertion compared to the case without the presence of delayed neutrons, where the reactor period was 1 second.
Reactor Period – SUR – Doubling Time
Reactor Period
Reactivity is not directly measurable, and therefore most power reactors procedures do not refer to it, and most technical specifications do not limit it. Instead, they specify a limiting rate of neutron power rise (measured by excore detectors), commonly called a reactor period (especially in the case of BWRs).
The reactor period, τe, or e-folding time, is defined as the time required for the neutron density to change by a factor e = 2.718. The reactor period is usually expressed in units of seconds or minutes.
At this time:
where:
n(t) = transient reactor power
n(0) = initial reactor power
τe = reactor period
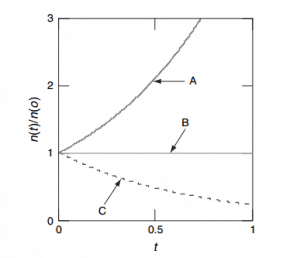
The smaller the value of τe, the more rapid the change in reactor power. The reactor period may be positive or negative. If the reactor period is positive, reactor power increases. If the reactor period is negative, reactor power decreases. Suppose the reactor period is constant with time, as associated with exponential power change. In that case, the rate is a stable reactor period if the reactor period is not constant but is changing with time. For non-exponential power change, the period is referred to as a transient reactor period.
Derivation of the formula τe = ld / (k-1) is based on many assumptions, and it is the simplest approximation of the reactor period. A much more exact formula reactor period is based on solutions of six-group point kinetics equations. From this equation, an equation called the inhour equation (which comes from the inverse hour, when it was used as a unit of reactivity that corresponded to e-fold neutron density change during one hour) may be derived.
where:
l = prompt neutron lifetime
βeff = effective delayed neutron fraction
λeff = effective delayed neutron precursor decay constant
τe = reactor period
ρ = reactivity
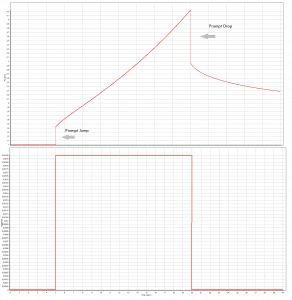
The first term in this formula is the prompt term, and it causes that the positive reactivity insertion is followed immediately by an immediate power increase called the prompt jump. This power increase occurs because the production rate of prompt neutrons changes immediately as the reactivity is inserted. After the prompt jump, the power change rate cannot increase any more rapidly than the built-in time delay the precursor half-lives allow. Therefore the second term in this formula is called the delayed term. The presence of delayed neutrons causes the power rise to be controllable, and the reactor can be controlled by control rods or another reactivity control mechanism.
The relationship between reactor period and startup rate is given by the following equations:
Example:
Suppose keff = 1.0005 in a reactor with a generation time ld = 0.01s. Calculate the reactor period – τe, doubling time – DT, and the startup rate (SUR) for this state.
ρ = 1.0005 – 1 / 1.0005 = 50 pcm
τe = ld / k-1 = 0.1 / 0.0005 = 200 s
DT = τe . ln2 = 139 s
SUR = 26.06 / 200 = 0.13 dpm
Doubling Time
Doubling time is a unit similar to radioactive decay calculations. Doubling is defined as the amount of time it takes reactor power to double the initial power level. The reactor period is usually expressed in units of seconds or minutes. If the reactor period is known, doubling time can be determined as follows.
Doubling time = τe . ln2
where:
τe = reactor period
ln2 = natural logarithm of 2
The smaller the value of DT, the more rapid the change in reactor power. The doubling time may be positive or negative. If the doubling time is positive, reactor power is increasing. If the value is negative, we talk about the halving time, and reactor power is decreasing.
Example:
Suppose keff = 1.0005 in a reactor with a generation time ld = 0.01s. Calculate the reactor period – τe, doubling time – DT, and the startup rate (SUR) for this state.
ρ = 1.0005 – 1 / 1.0005 = 50 pcm
τe = ld / k-1 = 0.1 / 0.0005 = 200 s
DT = τe . ln2 = 139 s
SUR = 26.06 / 200 = 0.13 dpm
Startup Rate – SUR
Reactivity is not directly measurable, and therefore most power reactors procedures do not refer to it, and most technical specifications do not limit it. Instead, they specify a limiting rate of neutron power rise (measured by excore detectors), commonly called a startup rate (especially in the case of PWRs).
The reactor startup rate is defined as the number of factors often that power changes in one minute. Therefore the units of SUR are powers of ten per minute or decades per minute (dpm). The relationship between reactor power and startup rate is given by the following equation:
n(t) = n(0).10SUR.t
where:
SUR = reactor startup rate [dpm – decades per minute]
t = time during reactor transient [minute]
The higher the value of SUR, the more rapid the change in reactor power. The startup rate may be positive or negative. If SUR is positive, reactor power is increasing. If SUR is negative, reactor power is decreasing. The relationship between reactor period and startup rate is given by the following equations:
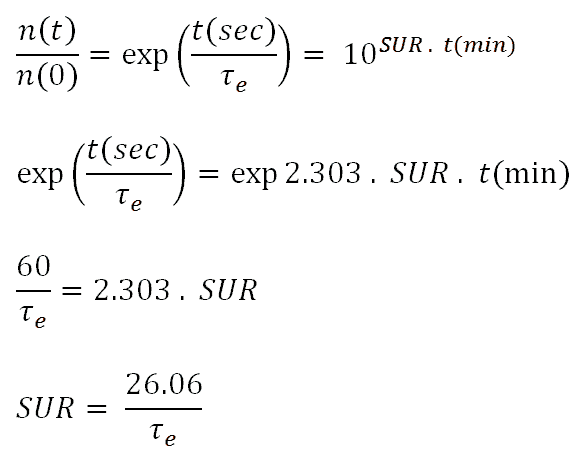
Example:
Suppose keff = 1.0005 in a reactor with a generation time ld = 0.01s. Calculate the reactor period – τe, doubling time – DT, and the startup rate (SUR) for this state.
ρ = 1.0005 – 1 / 1.0005 = 50 pcm
τe = ld / k-1 = 0.1 / 0.0005 = 200 s
DT = τe . ln2 = 139 s
SUR = 26.06 / 200 = 0.13 dpm
Effect of Presence of Delayed Neutrons
