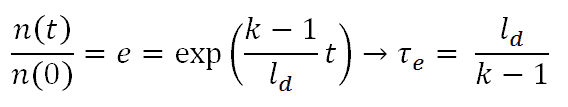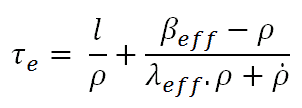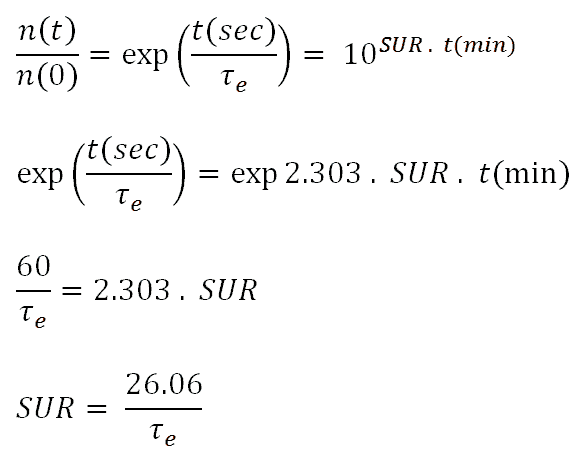Reactor Period

Reactivity is not directly measurable, and therefore most power reactors procedures do not refer to it, and most technical specifications do not limit it. Instead, they specify a limiting rate of neutron power rise (measured by excore detectors), commonly called a reactor period (especially in the case of BWRs).

The reactor period, τ_e, or e-folding time, is defined as the time required for the neutron density to change by a factor e = 2.718. The reactor period is usually expressed in units of seconds or minutes.

At this time:

where:
n(t) = transient reactor power
n(0) = initial reactor power
τ_e = reactor period

The smaller the value of τ_e, the more rapid the change in reactor power. The reactor period may be positive or negative. If the reactor period is positive, reactor power increases. If the reactor period is negative, reactor power decreases. If the reactor period is constant with time, as associated with exponential power change, the rate is a stable reactor period. If the reactor period is not constant but is changing with time, for non-exponential power change, the period is referred to as a transient reactor period.

Derivation of the formula τ_e = l_d / (k-1) is based on many assumptions, and it is the simplest approximation of the reactor period. A much more exact formula reactor period is based on solutions of six-group point kinetics equations. An equation called the inhour equation (which comes from an inverse hour, used as a unit of reactivity that corresponded to e-fold neutron density change during one hour) might be derived.

where:
l = prompt neutron lifetime
β_eff = effective delayed neutron fraction
λ_eff = effective delayed neutron precursor decay constant
τ_e = reactor period
ρ = reactivity

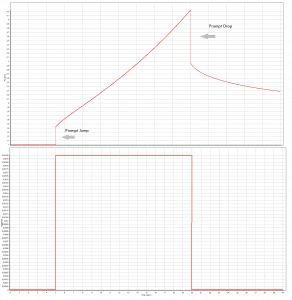
Prompt Jump - Prompt Drop — The presence of delayed neutrons brings many interesting phenomena. This chart shows the typical response of the reactor on constant reactivity insertion.

The first term in this formula is the prompt term, and it causes that the
positive reactivity insertion is followed immediately by an immediate power increase called the prompt jump. This power increase occurs because the production rate of prompt neutrons
changes immediately as the reactivity is inserted. After the prompt jump, the power change rate cannot increase any more rapidly than the built-in time delay the precursor half-lives allow. Therefore the second term in this formula is called the delayed term. The presence of delayed neutrons causes the power rise to be controllable, and the reactor can be controlled by control rods or another reactivity control mechanism.

The following equations give the relationship between reactor period and startup rate:

Example:

Suppose k_eff = 1.0005 in a reactor with a generation time l_d = 0.01s. Calculate the reactor period – τ_e, doubling time – DT, and the startup rate (SUR) for this state.

ρ = 1.0005 – 1 / 1.0005 = 50 pcm

τ_e = l_d / k-1 = 0.1 / 0.0005 = 200 s

DT = τ_e . ln2 = 139 s

SUR = 26.06 / 200 = 0.13 dpm

References:

Nuclear and Reactor Physics:

J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See above:

Reactivity