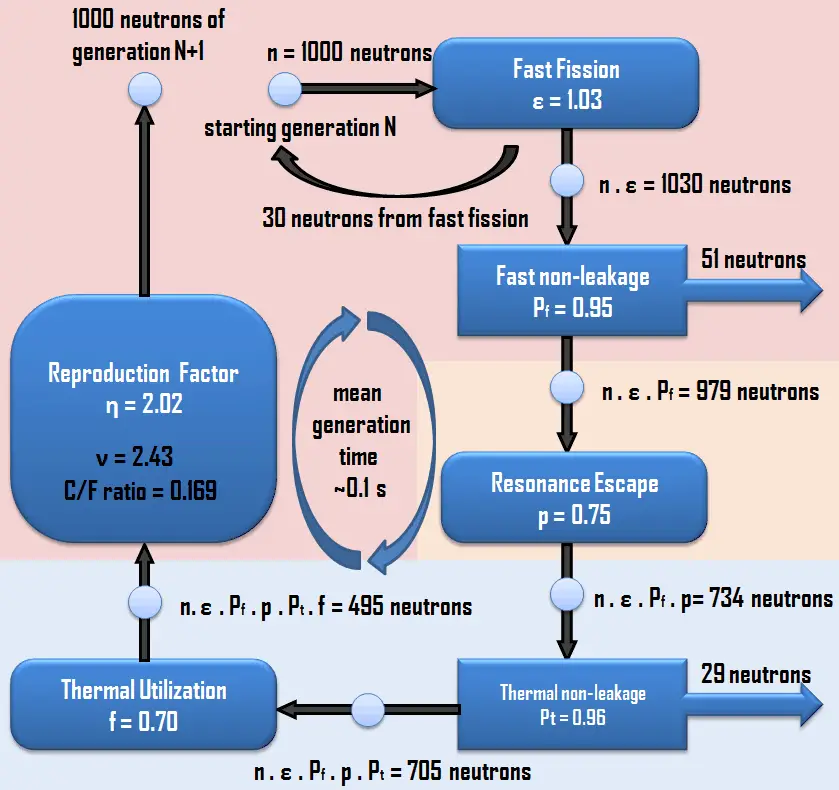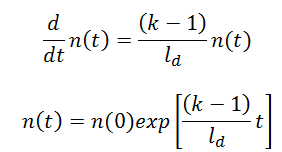
In the preceding chapters, the multiplication factors have been analyzed to understand a steady-state condition. Also, the operational changes that influence the criticality of the reactor were described. It must be noted and nuclear reactors are not always critical. The keff must be changed for a certain period to start or shut it down, which changes the neutron population in the reactor core. The study of the behavior of the neutron population in a noncritical reactor is called reactor kinetics. From this point of view, the state of a reactor can be distinguished by the following criteria.
The basic classification of states of a reactor is according to the multiplication factor as eigenvalue, which measures the change in the fission neutron population from one neutron generation to the subsequent generation.
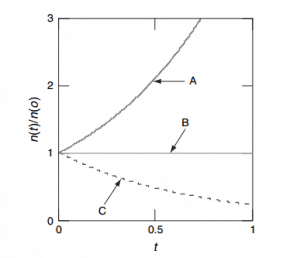
- keff < 1. Suppose the multiplication factor for a multiplying system is less than 1.0. In that case, the number of neutrons decreases in time (with the mean generation time), and the chain reaction will never be self-sustaining. This condition is known as the subcritical state.
- keff = 1. If the multiplication factor for a multiplying system is equal to 1.0, then there is no change in neutron population in time, and the chain reaction will be self-sustaining. This condition is known as the critical state.
- keff > 1. If the multiplication factor for a multiplying system is greater than 1.0, then the multiplying system produces more neutrons than are needed to be self-sustaining. The number of neutrons is exponentially increasing in time (with the mean generation time). This condition is known as the supercritical state.
The definitions described above are fully applicable to a reactor at zero power level, that is, at such a power level. All thermal considerations are not important to the chain reaction (from zero power to 1% of rated power).
keff = k∞ . Pf . Pt
If there are neutrons in the system at t=0, that is, if n(0) > 0, the solution of this equation gives the simplest point kinetics equation with delayed neutrons (similarly to the case without delayed neutrons):
Let us consider that the mean generation time with delayed neutrons is ~0.085 and k (k∞ – neutron multiplication factor) will be step increased by only 0.01% (i.e., 10pcm or ~1.5 cents), that is k∞=1.0000 will increase to k∞=1.0001.
It must be noted such reactivity insertion (10pcm) is very small in the case of LWRs. The reactivity insertions of the order of one pcm are for LWRs practically unrealizable. In this case, the reactor period will be:
T = ld / (k∞-1) = 0.085 / (1.0001-1) = 850s
This is a very long period. In ~14 minutes, the reactor’s neutron flux (and power) would increase by a factor of e = 2.718. This is a completely different dimension of the response on reactivity insertion compared to the case without delayed neutrons, where the reactor period was 1 second.
Reactors with such kinetics would be quite easy to control. From this point of view, it may seem that reactor control will be quite a boring affair. It will not! The presence of delayed neutrons entails many specific phenomena that will be described in later chapters.
Criticality of a Power Reactor – Power Defect
For power reactors, at power conditions, the reactor can behave differently due to the presence of reactivity feedbacks. Power reactors are initially started from hot standby mode (a subcritical state at 0% of rated power) to power operation mode (100% of rated power) by withdrawing control rods and boron dilution from the primary source coolant. During the reactor startup and up to about 1% of rated power, the reactor kinetics is exponential as in a zero-power reactor. This is due to the fact all temperature reactivity effects are minimal.
On the other hand, temperature reactivity effects play a very important role during further power increase from about 1% up to 100% of rated power. As the neutron population increases, the fuel and the moderator increase their temperature, which results in a decrease in reactivity of the reactor (almost all reactors are designed to have the temperature coefficients negative).
See also: Operational factors that affect the multiplication in PWRs.
The negative reactivity coefficient acts against the initial positive reactivity insertion, and this positive reactivity is offset by negative reactivity from temperature feedbacks. Positive reactivity must be continuously inserted (via control rods or chemical shim) to keep the power to be increasing. After each reactivity insertion, the reactor power stabilizes itself on the power level proportionately to the reactivity inserted. The total amount of feedback reactivity that must be offset by control rod withdrawal or boron dilution during the power increase is known as the power defect. The power defects for PWRs, graphite-moderated reactors and sodium-cooled fast reactors are:
- about 2500pcm for PWRs,
- about 800pcm for graphite-moderated reactors
- about 500pcm for sodium-cooled fast reactors
The power defects slightly depend on the fuel burnup because they are determined by the power coefficient, which depends on the fuel burnup. The power coefficient combines the Doppler, moderator temperature, and void coefficients. It is expressed as a change in reactivity per change in percent power, Δρ/Δ% power. The value of the power coefficient is always negative in core life. Still, it is more negative at the end of the cycle primarily due to the decrease in the moderator temperature coefficient.
It is logical, as power defects act against power increase, they also act against power decrease. When reactor power is decreased quickly, as in the reactor trip, power defect causes a positive reactivity insertion, and the initial rod insertion must be sufficient to make the reactor safe subcritical. Obviously, if the power defect for PWRs is about 2500pcm (about 6 βeff), the control rods must weigh more than 2500pcm to achieve the subcritical condition. The control rods must weigh more than 2500pcm plus the value of SDM (SHUTDOWN MARGIN) to ensure the safe subcritical condition. The total weight of control rods is design-specific, but, for example, it may reach about 6000pcm. They must be maintained above a minimum rod height (rods insertion limits) to ensure that the control rods can safely shut down the reactor.
Prompt Criticality
The basic classification of states of a reactor may be in some cases insufficient, and a finer classification is needed. The finer classification takes into account the two groups of neutrons that are produced in fission.
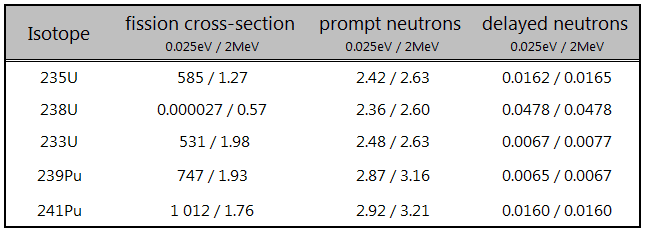
It is known the fission neutrons are of importance in any chain-reacting system. The fission of fissile nuclei produces 2, 3, or more free neutrons. But not all neutrons are released at the same time following fission. Even the nature of the creation of these neutrons is different. From this point of view, we usually divide the fission neutrons into two following groups:
- Prompt Neutrons. Prompt neutrons are emitted directly from fission, and they are emitted within a very short time of about 10-14 seconds.
- Delayed Neutrons. Delayed neutrons are emitted by neutron-rich fission fragments that are called delayed neutron precursors. These precursors usually undergo beta decay, but a small fraction of them are excited enough to undergo neutron emission. The neutron is produced via this type of decay, and this happens orders of magnitude later than the emission of the prompt neutrons, which plays an extremely important role in the control of the reactor.
The prompt neutrons are emitted within 10-14 and have significantly shorter mean generation time (~ 10-5s) than delayed neutrons (~0.1s) have crucial consequences. The period of ~10-5s is very short and causes a very fast response of the reactor power in case of prompt criticality. The state of a reactor, when the chain reaction is self-sustained only by prompt neutrons, is known as the prompt critical state. This state of the reactor is very unstable because one neutron generation takes only ~10-5s. Therefore nuclear reactors must operate in the prompt subcritical, delayed critical condition. All power reactors are designed to operate in delayed critical conditions and are provided with safety systems to prevent them from ever achieving prompt criticality.
The prompt critical state is defined as:
- keff > 1; ρ ≥ βeff, where the reactivity of a reactor is higher than the effectively delayed neutron fraction. In this case, the production of prompt neutrons alone is enough to balance neutron losses and increase the neutron population. The number of neutrons exponentially increases in time (as rapidly as the prompt neutron generation lifetime ~10-5s).
The prompt subcritical and delayed supercritical state is defined as:
- keff > 1; 0 < ρ < βeff, where the reactivity of a reactor is higher than zero and lower than the effectively delayed neutron fraction. In this case, the production of prompt neutrons alone is insufficient to balance neutron losses, and the delayed neutrons are needed to sustain the chain reaction. The neutron population increases, but much more slowly (as the mean generation lifetime with delayed neutrons ~0.1 s).
The prompt subcritical and delayed critical state is defined as:
- keff = 1; ρ = 0, where the reactivity of a reactor is equal to zero. In this case, the production of prompt neutrons alone is insufficient to balance neutron losses, and the delayed neutrons are needed to sustain the chain reaction. There is no change in neutron population in time, and the chain reaction will be self-sustaining. This state is the same state as the critical state from basic classification.
The prompt subcritical and delayed subcritical state is defined as:
- keff < 1; ρ < 0, where the reactivity of a reactor is lower than zero. In this case, the production of all neutrons is insufficient to balance neutron losses, and the chain reaction is not self-sustaining. If the reactor core contains external or internal neutron sources, the reactor is in the state that is usually referred to as the subcritical multiplication.
The effectively delayed neutron fraction reflects the ability of the reactor to thermalize and utilize each neutron produced. The β is not the same as the βeff due to the fact delayed neutrons do not have the same properties as prompt neutrons released directly from fission. In general, delayed neutrons have lower energies than prompt neutrons. Prompt neutrons have initial energy between 1 MeV and 10 MeV, with an average energy of 2 MeV. Delayed neutrons have initial energy between 0.3 and 0.9 MeV with an average energy of 0.4 MeV.
Therefore, in thermal reactors, a delayed neutron traverses a smaller energy range to become thermal. It is also less likely to be lost by leakage or parasitic absorption than the 2 MeV prompt neutron. On the other hand, delayed neutrons are also less likely to cause fast fission because their average energy is less than the minimum required for fast fission to occur.
These two effects (lower fast fission factor and higher fast non-leakage probability for delayed neutrons) tend to counteract each other and form a term called the importance factor (I). The importance factor relates the average delayed neutron fraction to the effectively delayed neutron fraction. As a result, the effectively delayed neutron fraction is the product of the average delayed neutron fraction and the importance factor.
βeff = β . I
The delayed and prompt neutrons have a difference in their effectiveness in producing a subsequent fission event. Since the energy distribution of the delayed neutrons also differs from group to group, the different groups of delayed neutrons will also have different effects. Moreover, a nuclear reactor contains a mixture of fissionable isotopes. Therefore, the important factor is insufficient in some cases, and an important function must be defined.
For example:
In a small thermal reactor with highly enriched fuel, the increase in fast non-leakage probability will dominate the decrease in the fast fission factor, and the important factor will be greater than one.
In a large thermal reactor with low enriched fuel, the decrease in the fast fission factor will dominate the increase in the fast non-leakage probability, and the important factor will be less than one (about 0.97 for a commercial PWR).
In large fast reactors, the decrease in the fast fission factor will also dominate the increase in the fast non-leakage probability, and the βeff is less than β by about 10%.
