Prompt Criticality
The basic classification of states of a reactor may be in some cases insufficient, and a finer classification is needed. The finer classification takes into account the two groups of neutrons that are produced in fission.
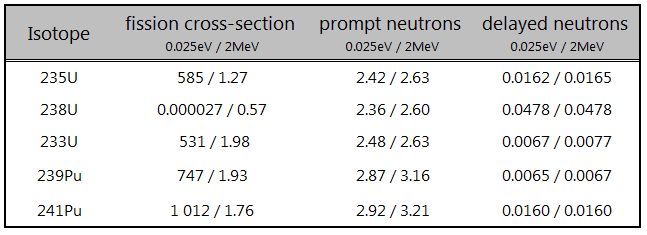
It is known the fission neutrons are of importance in any chain-reacting system. The fission of fissile nuclei produces 2, 3, or more free neutrons. But not all neutrons are released at the same time following fission. Even the nature of the creation of these neutrons is different. From this point of view, we usually divide the fission neutrons into two following groups:
- Prompt Neutrons. Prompt neutrons are emitted directly from fission, and they are emitted within a very short time of about 10-14 seconds.
- Delayed Neutrons. Delayed neutrons are emitted by neutron-rich fission fragments that are called delayed neutron precursors. These precursors usually undergo beta decay, but a small fraction of them are excited enough to undergo neutron emission. The neutron is produced via this type of decay, and this happens orders of magnitude later than the emission of the prompt neutrons, which plays an extremely important role in the control of the reactor.
The prompt neutrons are emitted within 10-14 and have significantly shorter mean generation time (~ 10-5s) than delayed neutrons (~0.1s) have crucial consequences. The period of ~10-5s is very short and causes a very fast response of the reactor power in case of prompt criticality. The state of a reactor, when the chain reaction is self-sustained only by prompt neutrons, is known as the prompt critical state. This state of the reactor is very unstable because one neutron generation takes only ~10-5s. Therefore nuclear reactors must operate in the prompt subcritical, delayed critical condition. All power reactors are designed to operate in delayed critical conditions and are provided with safety systems to prevent them from ever achieving prompt criticality. The prompt critical state is defined as:
- keff > 1; ρ ≥ βeff, where the reactivity of a reactor is higher than the effectively delayed neutron fraction. In this case, the production of prompt neutrons alone is enough to balance neutron losses and increase the neutron population. The number of neutrons exponentially increases in time (as rapidly as the prompt neutron generation lifetime ~10-5s).
The prompt subcritical and delayed supercritical state is defined as:
- keff > 1; 0 < ρ < βeff, where the reactivity of a reactor is higher than zero and lower than the effectively delayed neutron fraction. In this case, the production of prompt neutrons alone is insufficient to balance neutron losses, and the delayed neutrons are needed to sustain the chain reaction. The neutron population increases, but much more slowly (as the mean generation lifetime with delayed neutrons ~0.1 s).
The prompt subcritical and delayed critical state is defined as:
- keff = 1; ρ = 0, where the reactivity of a reactor is equal to zero. In this case, the production of prompt neutrons alone is insufficient to balance neutron losses, and the delayed neutrons are needed to sustain the chain reaction. There is no change in neutron population in time, and the chain reaction will be self-sustaining. This state is the same state as the critical state from basic classification.
The prompt subcritical and delayed subcritical state is defined as:
- keff < 1; ρ < 0, where the reactivity of a reactor is lower than zero. In this case, the production of all neutrons is insufficient to balance neutron losses, and the chain reaction is not self-sustaining. If the reactor core contains external or internal neutron sources, the reactor is in the state that is usually referred to as the subcritical multiplication.
The effectively delayed neutron fraction reflects the ability of the reactor to thermalize and utilize each neutron produced. The β is not the same as the βeff due to the fact delayed neutrons do not have the same properties as prompt neutrons released directly from fission. In general, delayed neutrons have lower energies than prompt neutrons. Prompt neutrons have initial energy between 1 MeV and 10 MeV, with an average energy of 2 MeV. Delayed neutrons have initial energy between 0.3 and 0.9 MeV with an average energy of 0.4 MeV.
Therefore, in thermal reactors, a delayed neutron traverses a smaller energy range to become thermal. It is also less likely to be lost by leakage or parasitic absorption than the 2 MeV prompt neutron. On the other hand, delayed neutrons are also less likely to cause fast fission because their average energy is less than the minimum required for fast fission to occur.
These two effects (lower fast fission factor and higher fast non-leakage probability for delayed neutrons) tend to counteract each other and form a term called the importance factor (I). The importance factor relates the average delayed neutron fraction to the effectively delayed neutron fraction. As a result, the effectively delayed neutron fraction is the product of the average delayed neutron fraction and the importance factor.
βeff = β . I
The delayed and prompt neutrons have a difference in their effectiveness in producing a subsequent fission event. Since the energy distribution of the delayed neutrons also differs from group to group, the different groups of delayed neutrons will also have different effectiveness. Moreover, a nuclear reactor contains a mixture of fissionable isotopes. Therefore, the important factor is insufficient in some cases, and an important function must be defined.
For example:
In a small thermal reactor with highly enriched fuel, the increase in fast non-leakage probability will dominate the decrease in the fast fission factor, and the important factor will be greater than one.
In a large thermal reactor with low enriched fuel, the decrease in the fast fission factor will dominate the increase in the fast non-leakage probability, and the important factor will be less than one (about 0.97 for a commercial PWR).
In large fast reactors, the decrease in the fast fission factor will also dominate the increase in the fast non-leakage probability, and the βeff is less than β by about 10%.
