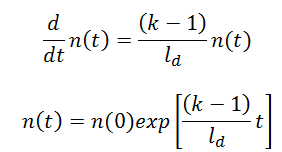Subcritical – Critical – Supercritical Reactor
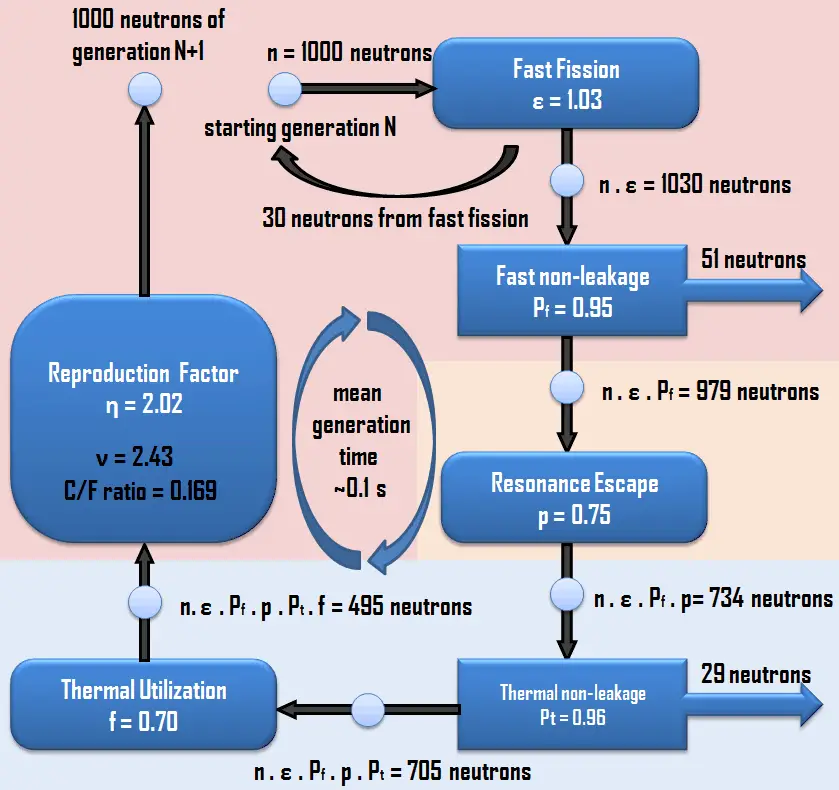
The basic classification of states of a reactor is according to the multiplication factor as eigenvalue, which measures the change in the fission neutron population from one neutron generation to the subsequent generation.
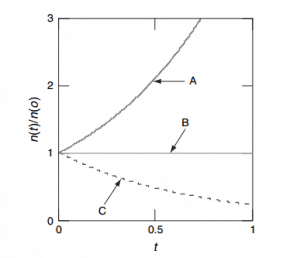
- keff < 1. Suppose the multiplication factor for a multiplying system is less than 1.0. In that case, the number of neutrons decreases in time (with the mean generation time), and the chain reaction will never be self-sustaining. This condition is known as the subcritical state.
- keff = 1. If the multiplication factor for a multiplying system is equal to 1.0, then there is no change in neutron population in time, and the chain reaction will be self-sustaining. This condition is known as the critical state.
- keff > 1. If the multiplication factor for a multiplying system is greater than 1.0, then the multiplying system produces more neutrons than are needed to be self-sustaining. The number of neutrons is exponentially increasing in time (with the mean generation time). This condition is known as the supercritical state.
The definitions described above are fully applicable to a reactor at zero power level, that is, at such a power level. All thermal considerations are not important to the chain reaction (from zero power to 1% of rated power).
See also: Criticality of Power Reactor
Prompt Criticality
The basic classification of states of a reactor may be insufficient, and a finer classification is needed. The finer classification takes into account the two groups of neutrons that are produced in fission.
The prompt critical state is defined as:
- keff > 1; ρ ≥ βeff, where the reactivity of a reactor is higher than the effectively delayed neutron fraction. In this case, the production of prompt neutrons alone is enough to balance neutron losses and increase the neutron population. The number of neutrons exponentially increases in time (as rapidly as the prompt neutron generation lifetime ~10-5s).
The prompt subcritical and delayed supercritical state is defined as:
- keff > 1; 0 < ρ < βeff, where the reactivity of a reactor is higher than zero and lower than the effectively delayed neutron fraction. In this case, the production of prompt neutrons alone is insufficient to balance neutron losses, and the delayed neutrons are needed to sustain the chain reaction. The neutron population increases, but much more slowly (as the mean generation lifetime with delayed neutrons ~0.1 s).
The prompt subcritical and delayed critical state is defined as:
- keff = 1; ρ = 0, where the reactivity of a reactor is equal to zero. In this case, the production of prompt neutrons alone is insufficient to balance neutron losses, and the delayed neutrons are needed to sustain the chain reaction. There is no change in neutron population in time, and the chain reaction will be self-sustaining. This state is the same state as the critical state from basic classification.
The prompt subcritical and delayed subcritical state is defined as:
- keff < 1; ρ < 0, where the reactivity of a reactor is lower than zero. In this case, the production of all neutrons is insufficient to balance neutron losses, and the chain reaction is not self-sustaining. If the reactor core contains external or internal neutron sources, the reactor is in the state that is usually referred to as the subcritical multiplication.