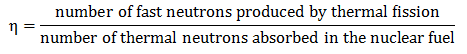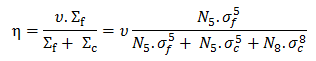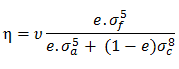The thermal utilization factor gives the fraction of the thermal neutrons absorbed in the nuclear fuel in all isotopes of the nuclear fuel. But the nuclear fuel is an isotopically rich material even in this case, in which we consider only the fissionable nuclei in the fuel. In the fresh uranium fuel, only three fissionable isotopes must be included in the calculations – 235U, 238U, 234U. In power reactors, the fuel significantly changes its isotopic content as the fuel burnup increases. The isotope of 236U and also trace amounts of 232U appears. The major consequence of increasing fuel burnup is that the content of the plutonium increases (especially 239Pu, 240Pu, and 241Pu). All these isotopes have to be included in the calculations of the reproduction factor.
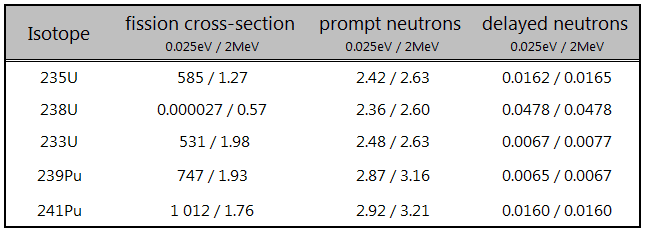
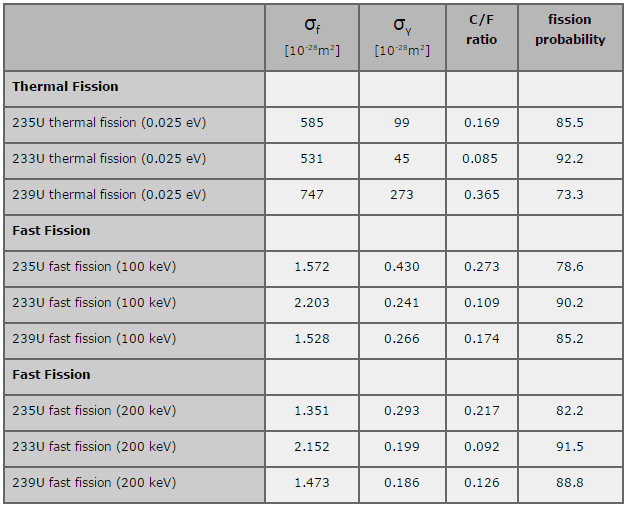
Another fact is that not all the absorption reactions that occur in the fuel result in fission. If we consider the thermal neutron and the nucleus of 235U, then about 15% of all absorption reactions result in radiative capture of a neutron. About 85% of all absorption reactions result in fission. Each fissionable nuclei have a different fission probability, and microscopic cross-sections determine these probabilities.
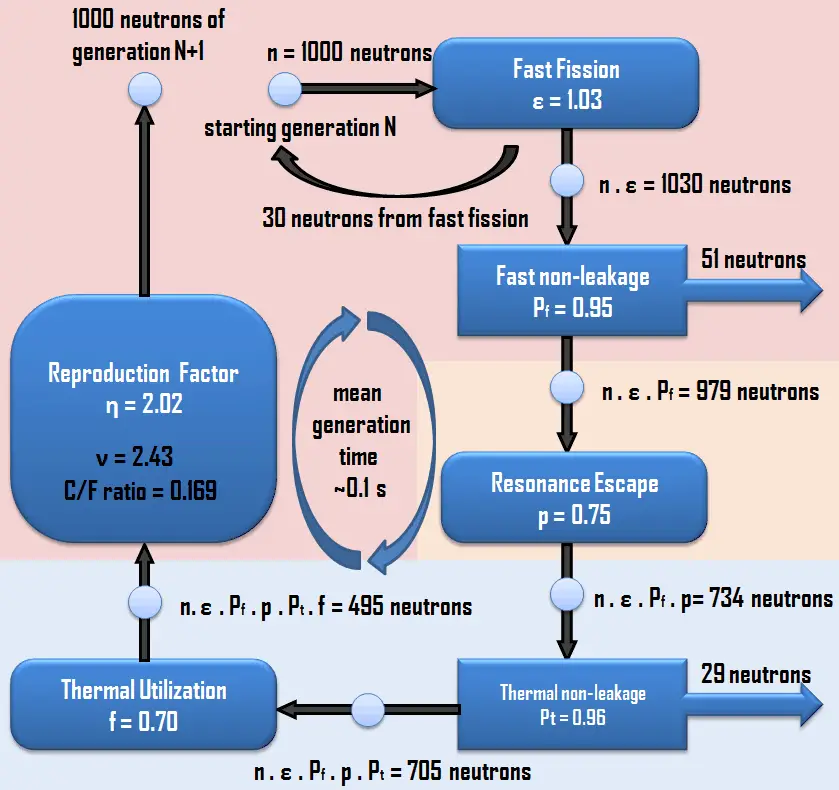
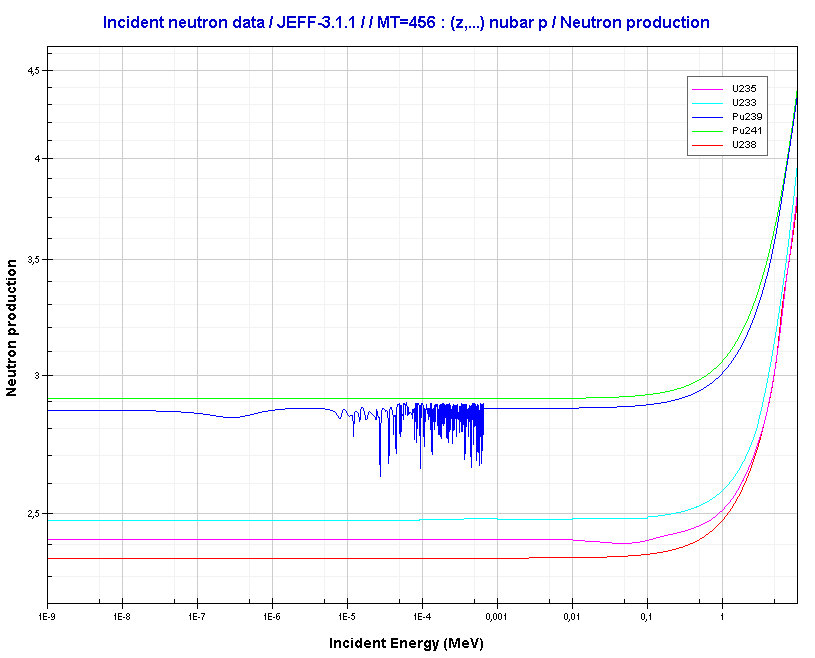
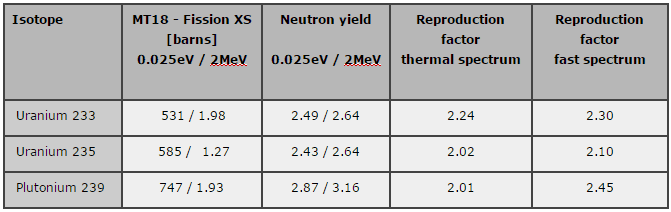
The neutrons finish one generation, and a new generation of neutrons may be created. The neutron reproduction factor determines the number of neutrons created in the new generation. The reproduction factor, η, is the ratio of the number of fast neutrons produced by thermal fission to the number
of thermal neutrons absorbed in the fuel. The reproduction factor is shown below.
495
↓
η ~ 2.02
↓
1000
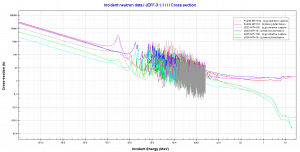The capture-to-fission ratio may be used as an indicator of “quality” of fissile isotopes. The ratio depends strongly on the incident neutron energy.
Source: JANIS (Java-based Nuclear Data Information Software); The JEFF-3.1.1 Nuclear Data Library
This factor is determined by the probability that fission reaction will occur times the average number of neutrons produced per one fission reaction. In the case of fresh uranium fuel, we consider only one fissile isotope, 235U, and the numerical value of η is given by the following equation:
in which ν is the average neutrons production of 235U, N5 and N8 are the atomic number densities of the isotopes 235U and 238U (when using other uranium isotopes or plutonium, the equation is modified trivially). This equation can also be written in terms of uranium enrichment:
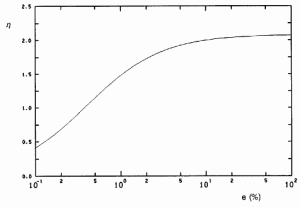
where e is the atomic degree of enrichment e = N5/(N5+N8), the reproduction factor is determined by the nuclear fuel composition and strongly depends on the neutron flux spectrum in the core, for natural uranium in the thermal reactor, η = 1.34. As a result of the ratios of the microscopic cross-sections, η increases strongly in the region of low enrichment fuels. This dependency is shown in the picture. It can be seen there is a limit value about η = 2.08.
Table of key prompt and delayed neutrons characteristics.
Source: JANIS (Java-based Nuclear Data Information Software); The JEFF-3.1.1 Nuclear Data Library
The numerical value of η does not change with core temperature over the range considered for most thermal reactors. There is essentially a small change in η over the lifetime of the reactor core (decreases). This is because there is a continuous decrease in ΣfU, but on the other hand, this decrease is partially offset by the increase in ΣfPu. As the fuel burnup increases, the 239Pu begins to contribute to the neutron economy of the core.
See also: Nuclear Breeding.
There are significant differences in reproduction factors between fast reactors and thermal reactors. The differences are in the number of neutrons produced per one fission and, of course, in neutron cross-sections that exhibit significant energy dependency. The differences in cross-sections can be characterized by the capture-to-fission ratio, which is lower in fast reactors. Furthermore, the number of neutrons produced per one fission is also higher in fast reactors than in thermal reactors. These two features are important in the neutron economy and contribute to the fact that fast reactors have a large excess of neutrons in the core.
