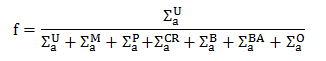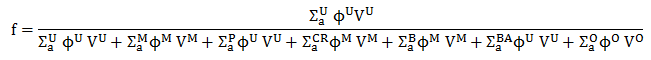Thermal Utilization Factor
Obviously, the neutrons that escape the resonance absorption and remain in the core will be thermalized. In thermal reactors, these neutrons continue to diffuse throughout the reactor until they are absorbed. But there are many materials in the reactor core in which these neutrons may be absorbed. The thermal utilization factor, f, is the fraction of the thermal neutrons absorbed in the nuclear fuel in all isotopes of the nuclear fuel. It describes how effectively (how well they are utilized) thermal neutrons are absorbed in the fuel.
The value of the thermal utilization factor is given by the ratio of the number of thermal neutrons absorbed in the fuel (all nuclides) to the number of thermal neutrons absorbed in all the material that makes up the core.
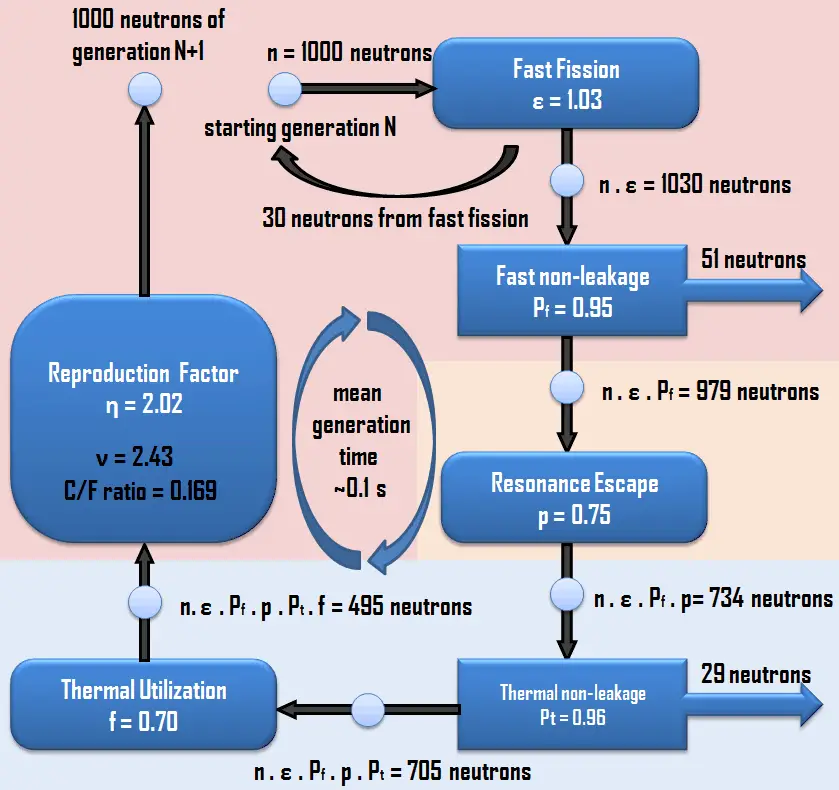
705
↓
f ~ 0.70
↓
495
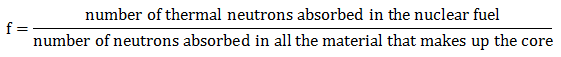
By definition, this factor will always be less than one because there will always be some of the thermal neutrons absorbed in non-fuel materials (usually referred to as parasitic absorption). For homogenous reactor cores, this factor can be calculated in terms of macroscopic cross-sections by the following equation:
where Σa is the macroscopic absorption cross-section, which is the sum of the capture cross-section and the fission cross-section, Σa = Σc + Σf. The superscripts U, M, P, CR, B, BA, and O, refer to uranium fuel, moderator, poisons, control rods, boric acid, burnable absorbers, etc. It is obvious that the presence of control rods, boric acid, or poisons causes a decrease in neutron utilization, which, in turn, causes a decrease in multiplication factor.
There is usually some difference between the neutron flux in the moderator and the neutron flux in the fuel in heterogeneous reactors. The high absorption in the fuel causes this difference, and the ratio of thermal neutron flux in the moderator to that in the fuel is known as the thermal disadvantage factor defined as:
The thermal utilization factor is for heterogeneous reactor cores about 0.5 – 0.8, but it depends strongly on the reactor type.
Main operational changes that affect this factor:
This factor is the key factor that the reactor operator has the greatest control over. Control rods insertion/withdrawal and borate/boron dilution from the moderator are operations, which influence precisely the thermal utilization factor. For example, control rods insertion causes the addition of new absorbing material into the core, and this causes a decrease in thermal utilization factor.
The thermal utilization factor slightly changes with the fuel burnup. The fresh fuel at the beginning of the cycle comprises only the absorption by the 235U. As the amount of 239Pu and other higher transuranic elements increases because of the radiative capture of a neutron by the 238U in the core, it is necessary to consider the change of fuel composition in determining the value of f at different times of the fuel cycle.
In general, the thermal utilization factor decreases in time as the total content of fissile isotopes decreases and the total content of neutron poisons (fission products with high absorption cross-sections) increases. But in the power reactors, in which the criticality must be maintained for a long period (e.g.,, 12-month or up to 24-month) without refueling, the thermal utilization factor may not decrease. Such a decrease would imply an inevitable reactor shutdown. The continuous decrease in ΣaU must be offset by the continuous decrease in ΣaB, which means the concentration of boric acid (in the case of PWRs) must be continuously decreased as the fuel loses its reactivity (kinf). For reactors in which the chemical shim can not be used, the excess of reactivity is compensated by compensating rods.
On the other hand, there is the fuel breeding, which plays very important role in the compensation of decreasing 235U content.
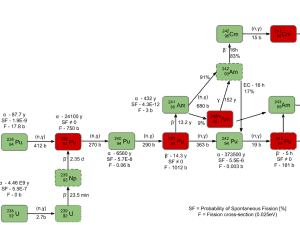Chain of the transuranic elements.
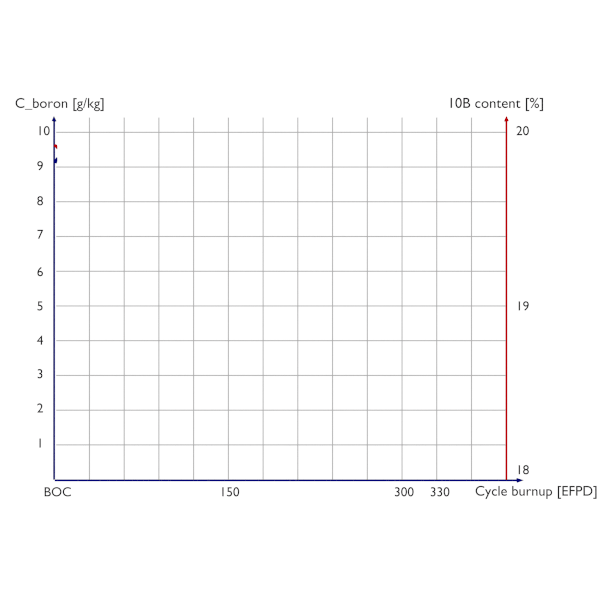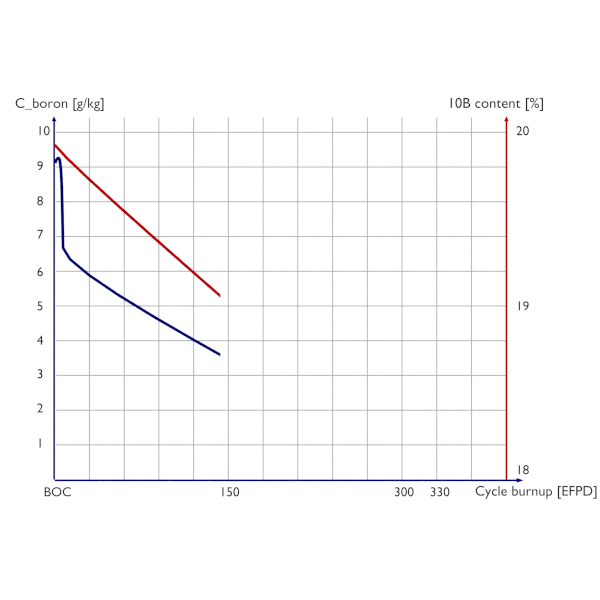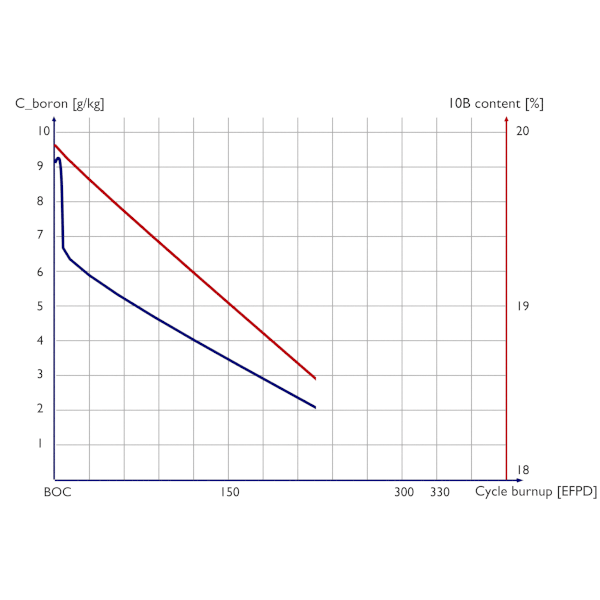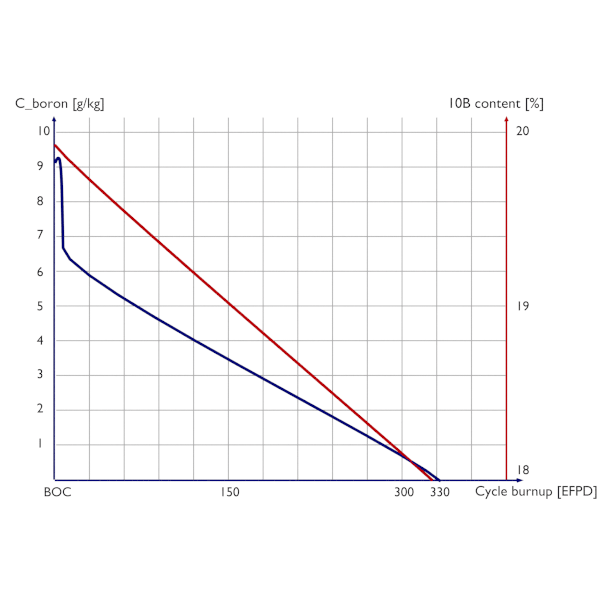Boron letdown curve (chemical shim) and boron 10 depletion during a 12-month fuel cycle.The fuel breeding in the fuel cycle of all commercial light water reactors plays a significant role. In recent years, the commercial power industry has been emphasizing high-burnup fuels (up to 60 – 70 GWd/tU), typically enriched to higher percentages of 235U (up to 5%). As burnup increases, a higher percentage of the total power produced in a reactor is due to the fuel bred inside the reactor.
At a burnup of 30 GWd/tU (gigawatt-days per metric ton of uranium), about 30% of the total energy released comes from bred plutonium. At 40 GWd/tU, that percentage increases to about forty percent. This corresponds to a breeding ratio for these reactors of about 0.4 to 0.5. That means about half of the fissile fuel in these reactors is bred there. This effect extends the cycle length for such fuels to sometimes nearly twice what it would be otherwise. MOX fuel has a smaller breeding effect than 235U fuel and is thus more challenging and slightly less economical to use due to a quicker drop-off in reactivity through cycle life.
Plutonium 239 breeding
Neutron capture may also be used to create fissile 239Pu from 238U, the dominant constituent of naturally occurring uranium (99.28%). Absorption of a neutron in the 238U nucleus yields 239U. The half-life of 239U is approximately 23.5 minutes. 239U decays (negative beta decay) to 239Np (neptunium), whose half-life is 2.36 days. 239Np decays (negative beta decay) to 239Pu.
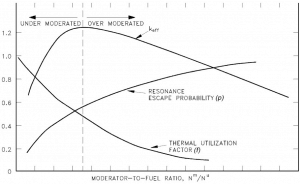The thermal utilization factor is dependent also on the moderator-to-fuel ratio – NM / NF. The change of the moderator-to-fuel ratio also changes the absorption by hydrogen atoms in the reactor core and simply changes the probability of absorption by fuel atoms.
Much more important, however, is the reactor design, which determines the moderator-to-fuel ratio. Most of light water reactors are designed as so called undermoderated with the slightly harder neutron flux spectrum (the moderation is slightly insufficient) than in an optimum case.