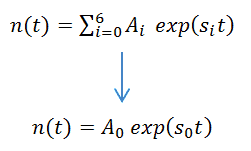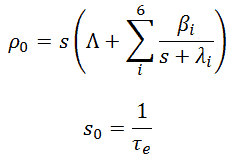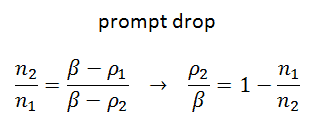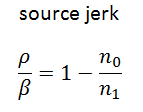Experimental Methods of Reactivity Determination

The asymptotic period measurement is based on measurement of exponential rise of neutron flux level during step increase in reactivity. In general, the stable reactor period (or asymptotic period), τ_e, is defined as the time required for the neutron density to change by a factor e = 2.718.

As was written in previous chapters, we can expect that the solution of point kinetics equation can be n(t) = A.exp(s.t) and C_i(t) = C_i,0.exp(s.t). In the asymptotic term (i.e., after the transition phenomena have died out), the asymptotic solution is in the form:

where s₀ = 1/_e is the stable reactor period or asymptotic period of the reactor. This root, s₀, is positive for ρ > 0 and negative for ρ < 0. Therefore this root describes the reactor response, lasting after the transition phenomena have died out. The measurement of the asymptotic period can be used to determine (directly from the inhour equation) the reactivity inserted into the system.

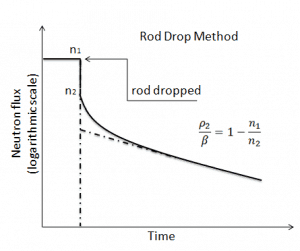The rod drop method belongs to a group of reactivity perturbation methods. This method is based on the study of the transient response of the reactor to a rapid insertion of high negative reactivity. This rapid reactivity insertion is usually performed by dropping the reactor control rods when the reactor is in a critical state. In this case, the reactivity inserted can be determined from the measurement of the prompt drop.

As was described in the Prompt Jump Approximation, the response of a neutron detector (n₁ ➝ n₂) immediately after a control rod is dropped into a critical reactor (ρ₁ = 0) is related by:

which allows the determination of the reactivity worth of the rod. The rod drop method is advantageous because it is very quick to perform and requires no extra equipment. Moreover, it can easily and safely measure large amounts of reactivity. On the other hand, the rod drop method is usually associated with reactor shutdown and subsequent reactor startup. Also, the rod drop time is not instantaneous as is theoretically assumed, therefore limiting the method’s accuracy. In PWRs, the drop time of all control rods is usually about 2 – 4 seconds.

This method is widely used to determine the worth of all control rods (i.e., of an emergency shutdown system). This method can also be used to determine the parameters of delayed neutrons, and these data can be obtained by decomposition of neutron flux coastdown.

A more accurate method is, for example, in:

Moore, K. V. Shutdown Reactivity by the Modified Rod Drop Method, USAEC Report ID0-16948, 1964.

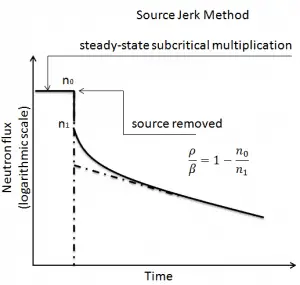The source jerk method belongs to a group of source perturbation methods. But in principle, the source jerk method is essentially the same as the rod drop method, except that it is a subcritical measurement, and the neutron source is removed instead of inserting a control rod. This method is based on the study of the transient response of the reactor to a rapid neutron source removal from a reactor.

In this case, the subcriticality of the reactor (subcritical multiplication) can be determined from the measurement of the prompt drop. Also, here the prompt drop can be measured because the delayed neutron precursor population will not change immediately. Following sudden source removal, the neutron population undergoes a sharp negative jump.

As was described in the Prompt Jump Approximation, the response of a neutron detector (n₁ ➝ n₂) immediately after a source removal from a subcritical reactor (ρ₁ < 0) is related by:

where n₀ is the neutron level with the source in place and n₁ is the neutron level immediately after the source jerk. Since a source is much smaller and lighter than a control rod, it is easier to quickly remove it from the core. On the other hand, in commercial reactors, this method cannot be used because, in commercial reactors, neutron sources (when used) cannot be simply removed from the core. Moreover, commercial reactors contain high burnup fuel, which is an important source of neutrons.

See also: Source Neutrons

Nuclear and Reactor Physics:

1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2. 
4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.