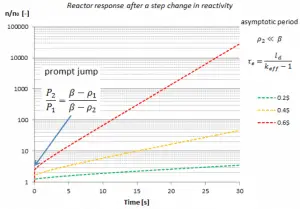
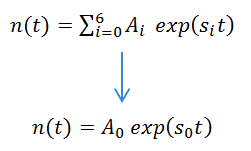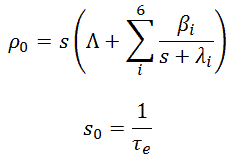 The asymptotic period measurement is based on measurement of exponential rise of neutron flux level during step increase in reactivity. In general, the stable reactor period (or asymptotic period), τe, is defined as the time required for the neutron density to change by a factor e = 2.718.
The asymptotic period measurement is based on measurement of exponential rise of neutron flux level during step increase in reactivity. In general, the stable reactor period (or asymptotic period), τe, is defined as the time required for the neutron density to change by a factor e = 2.718.
As was written in previous chapters, we can expect that the solution of point kinetics equation can be n(t) = A.exp(s.t) and Ci(t) = Ci,0.exp(s.t). In the asymptotic term (i.e., after the transition phenomena have died out) the asymptotic solution is in the form:
where s0 = 1/e is the stable reactor period or asymptotic period of reactor. This root, s0, is positive for ρ > 0 and negative for ρ < 0, therefore this root describes the reactor response, which is lasting after the transition phenomena have died out. The measurement of the asymptotic period can be used to determine (directly from the inhour equation) the reactivity inserted into the system.