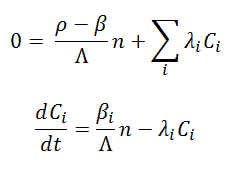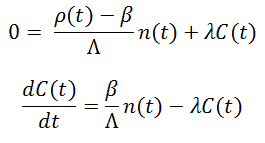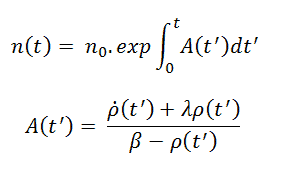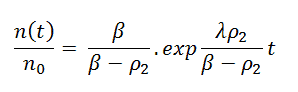 As can be seen from the solution of the exact point kinetics equation, any reactivity insertion (ρ < β) causes at first a sharp change in prompt neutrons population, and then the neutron response is slowed as a result of the more slowly changing number of delayed neutrons. The rapid response is a result of the small value of prompt neutron generation time in the denominator of the point kinetics equation.
As can be seen from the solution of the exact point kinetics equation, any reactivity insertion (ρ < β) causes at first a sharp change in prompt neutrons population, and then the neutron response is slowed as a result of the more slowly changing number of delayed neutrons. The rapid response is a result of the small value of prompt neutron generation time in the denominator of the point kinetics equation.
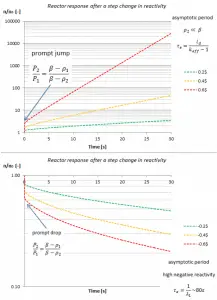
Suppose we are interested in long-term behavior (asymptotic period) and not interested in the details of the prompt jump. In that case, we can simplify the point kinetics equations by assuming that the prompt jump takes place instantaneously in response to any reactivity change. This approximation is known as the Prompt Jump Approximation (PJA). Due to prompt neutrons, the rapid power change is neglected, corresponding to taking dn/dt |0 = 0 in the point kinetics equations. That means the point kinetics equations are as follows:
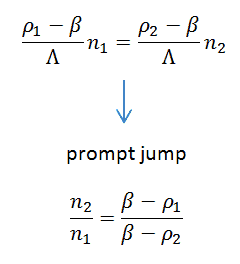
From the equation for neutron flux and the assumption that the delayed neutron precursor population does not respond instantaneously to a change in reactivity (i.e., Ci,1 = Ci,2), it can be derived that the ratio of the neutron population just after and before the reactivity change is equal to:
The prompt-jump approximation is usually valid for smaller reactivity insertion, for example, for ρ < 0.5β. It is usually used with another simplification and the one delayed precursor group approximation.
Prompt Jump Approximation with One Group of Delayed Neutrons
In the previous section, we have simplified the point kinetics equation using prompt jump approximation (PJA). This eliminated the fast time scale due to prompt neutrons. This section considers that delayed neutrons are produced only by one group of precursors with the same decay constant (averaged) and delayed neutron fraction. Point kinetics equation using PJA and one group of delayed neutrons becomes:
This simplification then leads to:
Assuming that the reactivity is constant and n1/n0 can be determined from the prompt jump formula, this equation leads to a very simple formula: