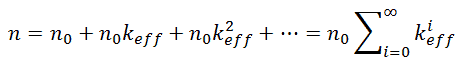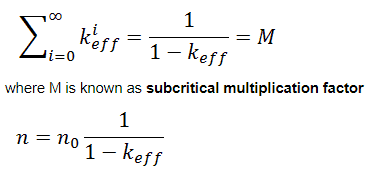Sb-Be neutron source is a typical external neutron source used in commercial nuclear reactors. It is usually loaded into fuel assemblies near the periphery of the core because the source-range excore detectors are installed outside the pressure vessel. Sb-Be source is a two-component source and, prior to irradiation, contains natural antimony (57.4% of 121Sb and 42.6% of 123Sb) and natural beryllium (100% of 9Be). The first component is a source of strong gamma rays, while the second is a neutron emitter element.
Thus the Sb-Be source is based on (γ,n) reaction (i.e., it emits photoneutrons). The neutron flux inside the core activates (σa = 0.02 barn) the isotope 123Sb resulting in 124Sb. 124Sb decays (with a half-life of 60.2 days) via beta decay to 124Te. The decay scheme of 124Sb shows two relevant groups of γ-ray energies, namely 1691 keV and 2091 keV, with absolute intensities of 0.484 and 0.057 per decay, respectively.
These γ-rays have sufficient energy to knock out a neutron from the second component, 9Be, which has the lowest threshold (1.66 MeV) for neutron emission. The (γ,n) source that uses antimony-124 as the gamma emitter is characterized in the following endothermic reaction.
124Sb→124Te + β− + γ
γ + 9Be→8Be + n – 1.66 MeV
The antimony-beryllium source produces nearly monoenergetic neutrons with the dominant peak at 23keV. Using the laws of energy and momentum conservation, one can derive that the 1691 keV and 2091 keV gamma rays produce two groups of neutrons:
- 23 keV (~97%)
- 378 keV (~3%)
Sb-Be sources have three main disadvantages:
- They have an extremely high photon to neutron ratio, complicating work with such sources.
- The yield of neutrons is significantly lower than for (α,n) sources. On the other hand, (α,n) sources contain transuranic elements such as americium which can be converted into fissile isotope 242mAm. These sources are not appropriate for commercial reactors.
- When loaded into a reactor, the Sb-Be source may contribute to the production of tritium. The most important source (due to releases of tritiated water) of tritium in nuclear power plants stems from boric acid. Still, it can also be produced from beryllium via the following sequence of reactions:
- 9Be(n,α)6He
- 6He →6Li + e– (β–; T1/2=0.8s)
- 6Li(n,α)3H
The geometry of Source Neutrons Assemblies
Since at PWRs, the source range neutron detectors are usually placed outside the reactor (excore). A source neutrons assemblies should be placed at least a few migration lengths from the core-periphery. The main reason is that source range detectors should not register primarily the source neutrons.
Source Neutrons and Subcritical Multiplication
Source neutrons play an important role in reactor safety, especially during shutdown state and reactor startup. Without source neutrons, there would be no subcritical multiplication, and the neutron population in the subcritical system would gradually approach zero. That means each neutron generation would have fewer neutrons than the previous one because keff is less than 1.0.
With source neutrons, the population remains at levels that can be measured by the source range of excore neutron detectors so that operators can always monitor how fast the neutron population is changing (can always monitor the reactivity of subcritical reactor). Note that if neutrons and fissionable material are present in the subcritical reactor, fission will occur (even a deep subcritical reactor will always produce a small number of fissions).
The source neutrons enter the life cycle and experience the same environment that fission neutrons experience. It must be noted source neutrons are produced at different energies (e.g., 24keV for Sb-Be source), usually below energies of fission neutrons.
When the reactor is made subcritical after operating at a critical state, the neutron population at first undergoes a prompt drop due to a rapid decrease in prompt neutrons. After a short time begins to decrease exponentially with a period corresponding to decay of the longest-lived delayed neutron precursors (i.e., ~ the 80s). With source neutrons, the neutron flux stabilizes itself at a corresponding level, determined by source strength, S, and the multiplication factor, keff.
For a defined source strength of n0 neutrons per neutron generation, the neutron population (i.e., the neutron flux) is given by:
where n0 is source neutrons (0. generation) and n0keffi are neutrons from i-th generation. As i goes to infinity, the sum of this geometric series is (for keff < 1):
As can be seen, the neutron population of a subcritical reactor with source neutrons does not drop to zero, the neutron population stabilizes itself at level n, which is equal to source multiplied by factor M.