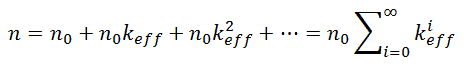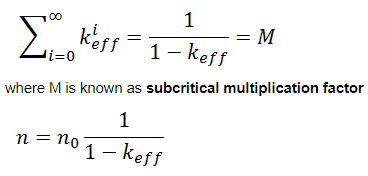Subcritical Multiplication Factor

For a defined source strength of n₀ neutrons per neutron generation, the neutron population (i.e., the neutron flux) is given by:

where, n₀ are source neutrons (0. generation) and n₀k_effⁱ are neutrons from i-th generation. As i goes to infinity, the sum of this geometric series is (for k_eff < 1):

As can be seen, the neutron population of a subcritical reactor with source neutrons does not drop to zero, the neutron population stabilizes itself at level n, which is equal to source multiplied by factor M.

Example: Subcritical Multiplication Factor

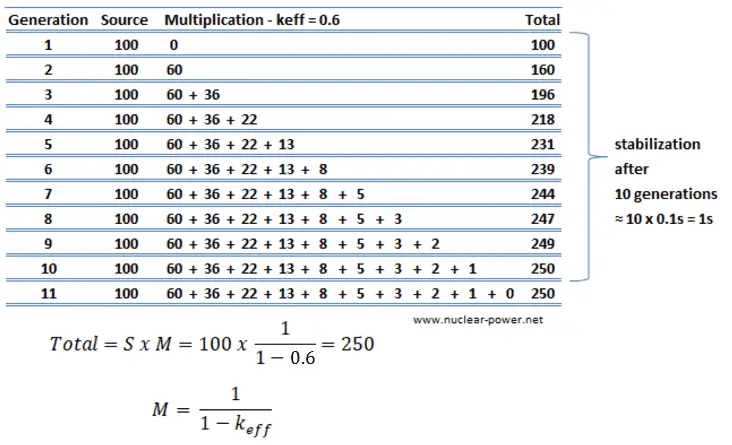
k_eff = 0.6

Consider a reactor in which:

• k_eff = 0.6
• the mean neutron generation to be l_d = 0.1s
• the external source provides n₀ = 100 neutrons/s.

When 100 neutrons are suddenly introduced into the reactor via source n₀, these neutrons will produce 60 neutrons (100 x 0.6) from fission to start the next generation. The duration of each neutron generation is equal to l_d = 0.1s. From 60 neutrons of the second generation, the system will produce 36 neutrons (60 x 0.6) to start the third generation (during l_d = 0.1s). The number of neutrons produced by fission in subsequent generations due to the introduction of 100 source neutrons into the reactor is shown in the figure.

As can be seen, the neutron population stabilizes itself at level n = 250, which is equal to source multiplied by factor M. The addition of source neutrons to the reactor containing fissionable material has the effect of maintaining a much higher stable neutron level due to the fissions occurring than the neutron level that would result from the source neutrons alone. As can be seen, the amount of time it takes to reach the steady-state neutron level is approximately equal to the time of 10 neutron generations (i.e., 10 x 0.1s = 1s).

Now, we will illustrate what happens to the neutron population when the value of k_eff is changed. For example, during a reactor startup, an initially subcritical reactor is driven to criticality via a series of discrete control rod withdrawals. During these withdrawals a reactivity increases. After each control rod withdrawal, the operator must wait to allow the reactor to attain the steady-state neutron level. The amount of time it takes to reach the steady-state neutron level after a reactivity change increases as k_eff approaches the critical state.

k_eff = 0.9

Consider a reactor in which:

• k_eff = 0.9
• the mean neutron generation to be l_d = 0.1s
• The external source provides n₀ = 100 neutrons/s.

When 100 neutrons are suddenly introduced into the reactor via source n₀, these neutrons will produce 90 neutrons (100 x 0.9) from fission to start the next generation. The duration of each neutron generation is equal to l_d = 0.1s. From 90 neutrons of the second generation, the system will produce 81 neutrons (90 x 0.9) to start the third generation (during l_d = 0.1s). The number of neutrons produced by fission in subsequent generations due to the introduction of 100 source neutrons into the reactor is shown in the figure.

As can be seen, the neutron population stabilizes itself at level n = 1000, which is equal to source multiplied by factor M. As can be seen, the amount of time it takes to reach the steady-state neutron level is significantly higher since it is approximately equal to the time of 50 neutron generations (i.e., 50 x 0.1s = 5s). The reason is evident in the series expression in the figure for k_eff = 0.9. As k_eff increases, more terms in the series are significant, meaning that more previous generations of source neutrons contribute to the present population.

Summary

Therefore, during a reactor startup, the value of k_eff increases and:

• the steady-state neutron level increases (by factor M)
• time of stabilization increases (let say 1/100 = k_effⁱ → t_stab = ln(0.01) / ln (k_eff) x l_d)

It must be noted, the real PWR cores reach reactivities around k_eff = 0.92 – 0.95 at the beginning of the reactor startup. Values around 0.6 are not common.

See above:

Subcritical Multiplication