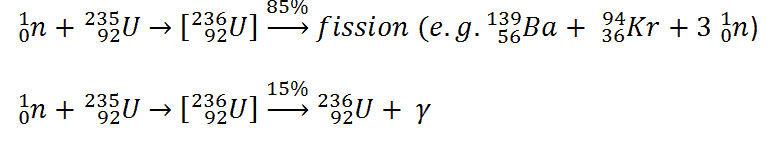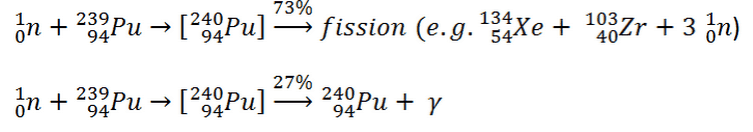Fuel Burnup

Units of Fuel Burnup

There are three different units in common use for describing the state or depletion of the fuel. These units are:

Megawatt-day per Metric Ton of Heavy Metal (unit: MWd/tHM)

In general, megawatt-day is a derived unit of energy. It is used to measure the energy produced, especially in power engineering. One megawatt day equals one megawatt of power produced by a power plant for one day (megawatts multiplied by the time in days). 1 MWd = 24,000 kWh.

At nuclear power plants, there are also gigawatt-days because it approximately corresponds to energy produced by power plants for one day. This unit (MWd) was also used to derive the unit of fuel burnup. The most commonly used measure of fuel burnup is the fission energy release per unit mass of fuel. Therefore fuel burnup of nuclear fuel normally has units of megawatt-days per metric tonne (MWd/MTU), where tonne refers to a metric ton of uranium metal (sometimes MWd/tU HM as Heavy Metal). In this field, the megawatt-day refers to the thermal power of the reactor, not the fraction which is converted to electricity. For example, for a typical nuclear reactor with thermal power of 3,000 MWth, about ~1,000 MWe of electrical power is generated in the generator.

For example, a reactor with 100,000 kg of fuel operating at a 3000 MWth power level for 1,000 days would have a burnup increase of 30,000 MWd/MTU. As was written, each watt of power production requires about 3.1×10¹⁰ fissions per second. In words of fissions, the fissioning of about 1 g of U-235 produces about 1 MWd of thermal energy (see: Energy Release per Fission).

Discharged fuel (i.e., after four years of operation) from light water reactors usually has a burnup of 45,000 to 50,000 MWd/tU. This means that about 45 to 50 kg of fissile material per metric ton of nuclear fuel used has been fissioned.

Burnup Fraction - Fission Burnup

Engineers sometimes use fission burnup or the burnup fraction as a useful unit of fuel burnup. This unit expresses the number of fission normalized to the initial number of uranium nuclei (or other fissionable nuclei). Fission burnup is the proportion of heavy nuclei placed in the reactor core that have undergone nuclear fission either directly or after conversion. In general, 1% in fission burnup is approximately equal to 10,000 MWd/tU.

Therefore, PWRs, which have an initial load of about 4% of uranium 235 (96% of uranium 238), reach about 4% of burnup fraction.

EFPD - Effective Full Power Day

A commonly used unit that describes the state of the fuel is the Effective Full Power Day (EFPD). It specifies the burnup of a given fuel assembly by the number of days it has resided in the core while the core was operated at full power. This unit is commonly used especially for cycle burnup description. For example, a typical 18-month fuel cycle requires an excess of reactivity for 500 EFPDs. It means the core must be refueled after 500 days at 100% rated power or after 1000 days at 50% rated power. The relation between EFPD and MWd/tU is:

Neutron Fluence

In nuclear engineering, we have to distinguish between the neutron flux density, the neutron intensity, and the neutron fluence.

Neutron fluence, previously referred to as the neutron dose, is defined as the time integral of the neutron flux density, expressed as the number of particles (neutrons) per cm². Neutron fluence is primarily defined for material engineering but is widely used by reactor engineers as a unit of fuel burnup.

Neutron Fluence and  Fuel Burnup – Neutrons per Kilobarn

Neutron fluence can be used to measure fuel burnup since the reaction rate is given by the product RR = Ф . Σ, the rate of burnup is proportional to the neutron flux. The accumulated burnup over a specific period (t) is therefore proportional to the product of flux and time (F = Ф . t or F = ∫Фdt). This product is known as the neutron fluence or the total neutron exposure of the fuel. The units of neutron fluence are also neutrons per m², but, in practice, it is often expressed in neutrons per kilobarn:

1 n/kb = 10²⁵ neutrons per m²

For example, let assume the fuel in PWR, which is irradiated with flux on the order of 3×10¹⁷ neutrons.m^-2s^-1 for approximately 4 years. The total fluence of discharged fuel is then 4 n/kb.

Neutron Fluence and Irradiation Embrittlement

During the nuclear power plant operation, the material of the reactor pressure vessel and the material of other reactor internals are exposed to neutron radiation (especially to fast neutrons), which results in localized embrittlement of the steel welds in the area of the reactor core. Irradiation embrittlement can lead to loss of fracture toughness. Typically, the low alloy reactor pressure vessel steels are ferritic steels that exhibit the classic ductile-to-brittle transition behavior with decreasing temperature. This transitional temperature is of the highest importance during plant heat up.

Failure modes:

• Low toughness region: Main failure mode is the brittle fracture (transgranular cleavage). In brittle fracture, no apparent plastic deformation takes place before fracture. Cracks propagate rapidly.
• High toughness region: Main failure mode is the ductile fracture (shear fracture). In ductile fracture, extensive plastic deformation (necking) occurs before fracture. Ductile fracture is better than brittle fracture because there is slow propagation and an absorption of a large amount of energy before fracture.

Neutron irradiation tends to increase the temperature (ductile-to-brittle transition temperature) at which this transition occurs and tends to decrease the ductile toughness.

Since the reactor pressure vessel is considered irreplaceable, neutron irradiation embrittlement of pressure vessel steels is a key issue in the long-term assessment of structural integrity for life attainment and extension programs.

Radiation damage is produced when neutrons of sufficient energy displace atoms (especially in steels at operating temperatures 260 – 300°C) that result in displacement cascades which produce large numbers of defects, both vacancies and interstitials. Although the inside surface of the RPV is exposed to neutrons of varying energies, the higher energy neutrons, those above about 0.5 MeV, produce the bulk of the damage. To minimize such material degradation type and structure of the steel must be appropriately selected. Today it is known that the susceptibility of reactor pressure vessel steels is strongly affected (negatively) by the presence of copper, nickel, and phosphorus.

To minimize neutron fluence:

• Radial neutron reflectors are installed around the reactor core. Neutron reflectors reduce neutron leakage, and therefore they reduce the neutron fluence on a reactor pressure vessel.
• Core designers design the low leakage loading patterns in which fresh fuel assemblies are not situated in the peripheral positions of the reactor core.

Heating the irradiated steel to a temperature sufficiently above the irradiation temperature can mitigate the embrittlement. At the normal operation of LWRs, the RPV material temperature is far from this temperature. Therefore, when it is required, plant operators must perform thermal annealing of irradiated reactor pressure vessel material to restore the mechanical properties. The degree of recovery for given steel depends on the time and the temperature at which annealing is performed.

See also: Integrity of reactor pressure vessels in nuclear power plants: assessment of irradiation embrittlement effects in reactor pressure vessel steels. International Atomic Energy Agency, ISBN 978-92-0-101709-3, Vienna, 2009.

Fuel Depletion – Isotopic Changes

As a reactor is operated at significant power, fuel atoms are constantly consumed, resulting in the slow depletion of the fuel. It must be noted there are also research reactors, which have very low power, and the fuel in these reactors does not change its isotopic composition.

Research reactors with significant thermal power and all power reactors are subjected to significant isotopic changes. The study of these isotopic changes is known as long-term kinetics, which describes phenomena that occur over months or even years. The study of phenomena that occur for several hours to a few days, for example, effects of neutron poisons on the reactivity (i.e., Xenon poisoning or spatial oscillations), is known as medium-term kinetics.
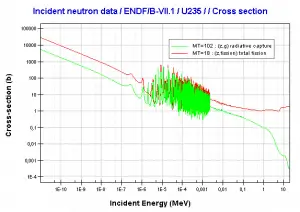
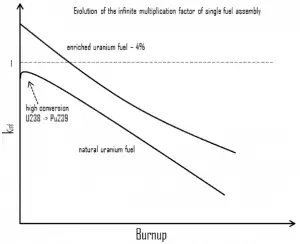
This chapter describes the long-term kinetics of thermal reactors based on the uranium fuel cycle, in which a fuel with a large concentration of uranium-238 is used (e.g., PWRs or BWRs). Most common reactor fuels are composed of either natural or partially enriched uranium. Typically, PWRs use enriched uranium fuel (~4% of U-235) as fresh fuel. Exposure to neutron flux gradually depletes the uranium-235, decreasing core reactivity (compensated by control rods, chemical shim, or burnable absorbers). The initial fuel load of a new reactor core (so-called first core) is entirely fresh fuel, fuel with no plutonium or fission products present. The contribution of uranium-238 directly to fission is quite small in most thermal reactors. On the other hand, uranium-238 plays a very important role, and this chapter is primarily about this isotope.

See also: Uranium

See also: Plutonium

Uranium 235

is a fissile isotope, and its fission cross-section for thermal neutrons is about 585 barns (for 0.0253 eV neutron). For fast neutrons, its fission cross-section is on the order of barns. Most absorption reactions result in fission reactions, but a minority results in radiative capture forming ²³⁶U. The cross-section for radiative capture for thermal neutrons is about 99 barns (for 0.0253 eV neutron). Therefore about 15% of all absorption reactions result in radiative capture of neutrons. About 85% of all absorption reactions result in fission.

Uranium 238

²³⁸U is a fissionable isotope but is not a fissile isotope. ²³⁸U cannot undergo a fission reaction after absorbing a thermal neutron. On the other hand, ²³⁸U can be fissioned by fast neutron with energy higher than >1MeV. During the fuel burning, the content of the U-235 continuously decreases, and the content of the plutonium increases (up to ~1% of Pu ). ²³⁸U also belongs to the group of fertile isotopes. Radiative capture of a neutron leads to the formation of fissile ²³⁹Pu and other transuranic elements. This is the way how ²³⁸U contributes to the operation of nuclear reactors and the production of electricity through this plutonium. For example, at a burnup of 40GWd/tU, about 40% of the total energy released comes from bred plutonium. This corresponds to a breeding ratio for this fuel burnup of about 0.4 to 0.5. That means about half of the fissile fuel in these reactors is bred there. This effect extends the cycle length for such fuels to nearly twice what it would otherwise be. MOX fuel has a smaller breeding effect than 235U fuel and is thus more challenging and slightly less economic to use due to a quicker drop-off in reactivity through cycle life.

Plutonium 239

Plutonium 239 is a fissile isotope, and its fission cross-section for thermal neutrons is about 750 barns (for 0.025 eV neutron). For fast neutrons, its fission cross-section is on the order of barns. Most of the absorption reactions result in fission reactions, but a part of reactions result in radiative capture forming ²⁴⁰Pu. The cross-section for radiative capture for thermal neutrons is about 270 barns (for 0.025 eV neutron). Therefore about 27% of all absorption reactions result in radiative capture of incident neutron. About 73% of all absorption reactions result in fission.

Plutonium 241

²⁴¹Pu is a fissile isotope, which means ²⁴¹Pu can undergo a fission reaction after absorbing a thermal neutron. Moreover, 241Pu also meets the alternative requirement that the amount of neutrons produced by fission of 241Pu (~2.94 per one fission by thermal neutron) is sufficient to sustain a nuclear fission chain reaction. Its fission cross-section for thermal neutrons is about 1012 barns (for 0.025 eV neutron). For fast neutrons, its fission cross-section is on the order of barns. Most absorption reactions result in fission reactions, but a part of reactions result in radiative capture forming ²⁴²Pu. The cross-section for radiative capture for thermal neutrons is about 363 barns (for 0.025 eV neutron). Therefore about 74% of all absorption reactions result in radiative capture of neutrons. About 26% of all absorption reactions result in fission. ²⁴¹Pu decays via beta decay into ²⁴¹Am with a half-life of only 14.3 years. ²⁴¹Am has relatively high cross-section for radiative capture for thermal neutrons (~680 barns – 0.025eV). These two phenomena (decrease in fissile isotope and increase in neutron absorber) cause a slight decrease in reactivity of irradiated fuel when stored in a spent fuel pool.

Nuclear Transmutation

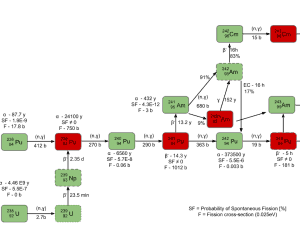In physics, nuclear transmutation is the conversion of one chemical element or an isotope into another. In nuclear engineering, also nuclear reactors cause artificial transmutation by exposing elements to neutrons produced by fission. In nuclear reactors, the most important phenomenon is the transmutation of fertile isotopes (e.g., uranium 238) into fissile isotopes (e.g., plutonium 239). The process of transmutation of fertile materials to fissile materials is referred to as fuel breeding.

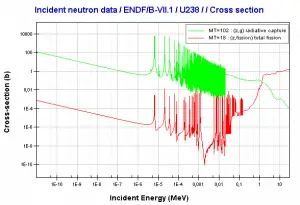
Fertile materials are not capable of undergoing fission reaction after absorbing thermal (slow or low energy) neutrons, and these materials are not capable of sustaining a nuclear fission chain reaction. There are two basic fertile materials: ²³⁸U and ²³²Th.

²³³U breeding:

²³²Th is the predominant isotope of natural thorium. If this fertile material is loaded in the nuclear reactor, the nuclei of ²³²Th absorb a neutron and become nuclei of ²³³Th. The half-life of ²³³Th is approximately 21.8 minutes. ²³³Th decays (negative beta decay) to ²³³Pa (protactinium), whose half-life is 26.97 days. ²³³Pa decays (negative beta decay)  to ²³³U, a very good fissile material. On the other hand, proposed reactor designs must attempt to physically isolate the protactinium from further neutron capture before beta decay can occur.

²³⁹Pu breeding:

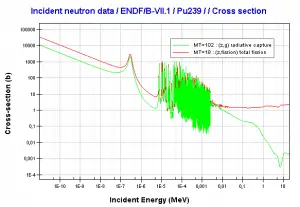
Neutron capture may also be used to create fissile ²³⁹Pu from ²³⁸U, the dominant constituent of naturally occurring uranium (99.28%). Absorption of a neutron in the ²³⁸U nucleus yields ²³⁹U. The half-life of ²³⁹U is approximately 23.5 minutes. ²³⁹U decays (negative beta decay) to ²³⁹Np (neptunium), whose half-life is 2.36 days. ²³⁹Np decays (negative beta decay)  to ²³⁹Pu.

Transmutation of transuranium elements (i.e., the chemical elements with atomic numbers greater than 92 ) such as the isotopes of plutonium can help solve some problems posed by the management of radioactive waste by reducing the proportion of long-lived isotopes it contains.

Evolution Equations

The same evolution of isotopic changes is usually modeled mathematically a set of differential equations known as evolution equations. These equations describe the rate of burnup of U-235, the rate of buildup of Pu-239, production of Pu-240 and Pu-241, the buildup of neutron-absorbing fission products and the overall rate of reactivity change in the reactor due to the changing composition of the fuel. The evolution equation can be constructed for each isotope. For example:

Special reference: W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.

Special reference: Paul Reuss, Neutron Physics, EDP Sciences, 2008, ISBN: 2759800415.

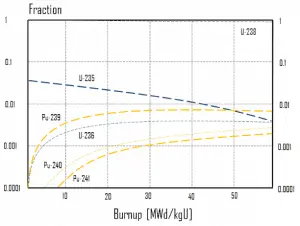
Isotopic Changes – Summary

In summary, it can be seen for fuel burnup of 40 GWd/tU:

• Approximately 3 – 4% of the heavy nuclei are fissioned.
• About two-thirds of these fissions come directly from uranium 235, and the other third comes from plutonium produced from uranium 238. The contribution significantly increases as the fuel burnup increases.
• The removed fuel (spent nuclear fuel) still contains about 96% reusable material. It must be removed due to decreasing k_inf of an assembly, or in other words, it must be removed due to accumulation of fission products with significant absorption cross-section.
• Discharged fuel contains about 0.8% of plutonium and about 1% of uranium 235. It must be noted there is a significant content (about 0.5%) of uranium 236, which is neither a fissile isotope nor a fertile isotope.

Neutron Poisons – Reactor Poisoning

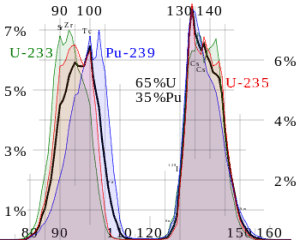
Nuclear fission fragments are the fragments left after a nucleus fissions. The average of the fragment mass is about 118, but very few fragments near that average are found. It is much more probable to break up into unequal fragments, and the most probable fragment masses are around mass 95 (Krypton) and 137 (Barium). Most of these fission fragments are highly unstable (radioactive) and undergo further radioactive decays to stabilize themselves.

Plenty of isotopes, usually neutron-rich isotopes, are produced by fission. Many of the resulting fission products have measurable thermal absorption cross-sections. Fission products are of concern in reactors primarily because they become parasitic absorbers of neutrons and result in long-term sources of heat (so-called decay heat). Their buildup in the reactor tends to reduce the multiplication factor. For that reason, these nuclei are known as neutron poisons.

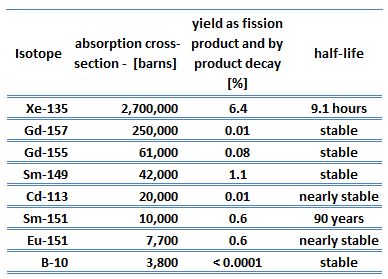
Each poison’s significance depends on the yield, decay rates, and absorption cross-section. Equilibrium is eventually reached during reactor operation if a radioisotope is produced constantly. After several half-lives, the rate of decay will equal the production rate. Most fission products have a low absorption cross-section, but there are very important exceptions. These isotopes are described in the following table.

As can be seen, most of these isotopes are stable, and some undergo decay. From this point of view, we distinguish between neutron poisons, which causes reactor poisoning, and neutron poisons, which cause reactor slagging.

The isotope with a short half-life (e.g., xenon-135) is known as reactor poison, while the isotope that is long-lived or even stable is known as reactor slag. The neutron-absorbing fission products xenon-135 and samarium-149 have particular operational importance.

Their concentrations can change quickly, producing major changes in neutron absorption on a relatively short time scale. Because these two fission product poisons remove neutrons from the reactor, they will impact the thermal utilization factor and thus k_eff and reactivity. The importance of xenon-135 and samarium-149 is so high that they will be discussed separately.

It must be noted that neutron-absorbing materials, also called neutron poisons, are intentionally inserted into some types of reactors to lower the high reactivity of their initial fresh fuel load. Some of these poisons deplete as they absorb neutrons during reactor operation, while others remain relatively constant.

Reactor Slagging – Reactor Slag

As was written, an isotope long-lived or even stable is known as reactor slag. The accumulation of these parasitic absorbers is known as reactor slagging and determines the lifetime of nuclear fuel in a reactor. Their buildup causes (together with a decrease in fissile material) a continuous decrease in core reactivity.

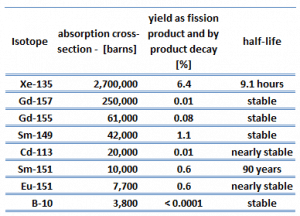Samarium 149 belongs to this group of isotopes, but its importance is so high that it is usually discussed separately. As can be seen from the table, there are numerous other fission products that, due to their concentration and thermal neutron absorption cross-section, have a poisoning effect on reactor operation. Other fission products with relatively high absorption cross-sections include ⁸³Kr, ⁹⁵Mo, ¹⁴³Nd, ¹⁴⁷Pm. Individually, they are of little consequence but taken together, and they have a significant effect. These are often characterized as lumped fission product poisons.

As was written, for fuel burnup of 40 GWd/tU, approximately 3 – 4% of the heavy nuclei are fissioned. The discharged fuel (spent nuclear fuel) still contains about 96% reusable material. It must be removed due to decreasing k_inf of an assembly or in or in other words, and it must be removed due to:

• accumulation of fission products with significant absorption cross-section.
• decrease in fissile material

This is the reason why some nuclear power plant operators use reprocessed fuel to replace fresh uranium fuel partially. Nuclear reprocessing is the technology that was developed to chemically separate and recover fissionable material from spent nuclear fuel as well as to remove these isotopes with significant absorption cross-section.

Effect of Fuel Depletion on the Power Distribution

During the operation of a reactor, the amount of fissile material contained in the fuel assembly constantly decreases; therefore, the assembly k_inf constantly decreases. During fuel depletion, the decrease of the assembly k_inf will be greatest where the power is greatest. The differences in k_inf between fresh fuel assemblies and high-burnup assemblies decreases. Therefore during cycle depletion, this process will cause the power to shift away from regions with the highest k_inf. This process also depends on the use of burnable absorbers, which disrupt the first assumption about the constantly decreasing assembly k_inf.

Effect of Fuel Depletion on Delayed Neutrons

In LWRs, the delayed neutron fraction decreases with fuel burnup. This is due to isotopic changes in the fuel. It is simple, and fresh uranium fuel contains only ²³⁵U as the fissile material, meanwhile during fuel burnup, the importance of fission of ²³⁹Pu increases (in some cases up to 50%). Since ²³⁹Pu produces significantly less delayed neutrons (0.0021 vs. 0.0064), the resultant core delayed neutron fraction of a multiplying system decreases (the weighted average of the constituent delayed neutron fractions). It follows then that the amount of reactivity insertion needed to produce a given reactor period decreases with the burnup of the fuel. This is also the reason why the neutron spectrum in the core becomes harder with fuel burnup.

β_core= ∑ P_i.β_i

where P_i is the fraction of power generated by isotope i.

Reactivity Effects of Fuel Burnup

↑burnup ⇒ ↓k_eff = ↓η  .ε.p.  ↓f  .  ↑↓P_f.  ↑↓P_t

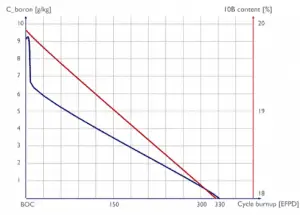
It is hard to describe the effects of fuel burnup on the six-factor formula, and it must be noted that criticality must be maintained for a long period. Therefore all the negative effects must be compensated by increasing the thermal utilization factor (boron dilution or compensating rods withdrawal).

See more: Operational factors that affect the multiplication

Neutron Flux Effects of Fuel Burnup

In a power reactor over a relatively short period (days or weeks), the atomic number density of the fuel atoms remains relatively constant. Therefore, the average neutron flux remains constant in this short period when the reactor is operated at a constant power level. On the other hand, the atomic number densities of fissile isotopes for months decrease due to the fuel burnup, and the macroscopic cross-sections decrease. Note that the thermal power is determined by reaction rate (RR = Ф . Σ), in which Σ is continuously decreasing. This result is slow to increase the neutron flux to keep the desired power level.

LWR with High Burnup Fuel

Current light water reactors are typically designed to achieve burnup of about 50 GWd/tU. With newer fuel technology, and particularly the use of advanced burnable absorbers, these same reactors can achieve up to 60 GWd/tU. Some studies show that soon, even with the present enrichment limit (5 wt %), fuel burnup could be extended near to 70 MWd/kg. Further increase in fuel burnup is impossible without the relaxation of the present enrichment limit (5%).

As can be seen, there has been a clear trend over the last decades toward increasing fuel burnup in light water reactors. In nuclear power plants, high fuel burnup is desirable for:

• Reducing the number of fresh nuclear fuel assemblies required and thus reducing spent nuclear fuel assemblies generated. Both aspects lead to improvements in the economics of the fuel cycle.
• Reducing the duration of refueling outage.
• High burnup results in a lower mass of spent fuel discharged per unit of electricity generated, reducing spent fuel handling and transportation.
• A benefit (crucial aspect for some operators) is that loading the “high” burnup assemblies in the periphery reduces the neutron flux on the pressure vessel.
• Reducing the potential for diversion of fissile material from spent fuel for non-peaceful.

On the other hand, some signals increasing burnup above 50 or 60 GWd/tU leads to significant engineering challenges, and even it does not necessarily have to lead to economic benefits.

See also: Etienne Parent. Nuclear Fuel Cycles for Mid-Century Deployment. MIT. 2009.

Higher burnup fuels require higher initial enrichment to sustain reactivity. Since the number of separative work units (SWUs) is not a linear enrichment function, it is more expensive to enrich higher enrichments. For instance, to produce one kilogram of uranium enriched to:

• 5% U-235 requires 8.9 SWU if the tails assay is 0.20%
• 4% U-235 requires 6.3 SWU if the tails assay is 0.20%

But there are also operational aspects of high burnup fuels that are associated especially with the reliability of such fuel. The main concerns associated with high burnup of fuels are:

• Increased burnup places additional demands on fuel cladding, which must withstand the reactor environment for a longer period.
• The longer residence in the reactor requires a higher corrosion resistance.
• Higher burnup leads to a higher accumulation of gaseous fission products inside the fuel pin resulting in a significant increase in internal pressure.
• Higher burnup leads to increased radiation-induced growth, leading to undesirable changes in core geometry (fuel assembly bow or fuel rod bow). FA bow can result in an increased control rods drop time due to friction between the control rod and bowed guide tubes.
• These factors must be considered because they can lead to a decrease in operational reliability.
• High burnup fuel generates a smaller fuel volume for the reprocessing but more specific activity.

Strategic management and decision-making regarding the middle part of nuclear fuel cycles is a very specific problem of power engineering. Such evaluation must also contain nuclear calculations and business-economic evaluation; thus, they cannot be carried out separately. Detailed nuclear calculations are necessary because they can exclude many promising strategies. On the other hand, they do not provide any information about benefits or costs. Strategic decision-making must be carried out based on business-economic evaluations.

Special reference: Technical and economic limits to fuel burnup extension, Proceedings of a Technical Committee meeting, IAEA, 11/2009