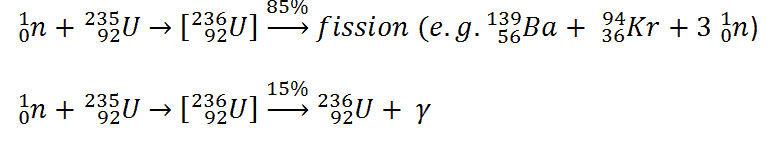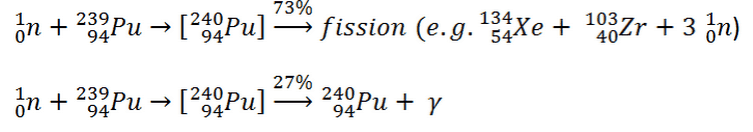
As a reactor is operated at significant power, atoms of fuel are constantly consumed, resulting in the slow depletion of the fuel. It must be noted there are also research reactors, which have very low power, and the fuel in these reactors does not change its isotopic composition.
Research reactors with significant thermal power and all power reactors are subjected to significant isotopic changes. The study of these isotopic changes is known as long-term kinetics, which describes phenomena that occur over months or even years. The study of phenomena that occur for several hours to a few days, for example, effects of neutron poisons on the reactivity (i.e., Xenon poisoning or spatial oscillations), is known as medium-term kinetics.
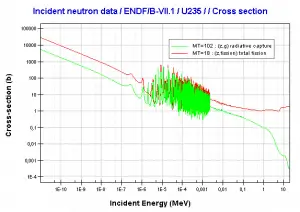
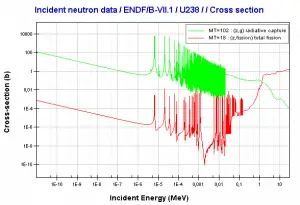
This chapter describes the long-term kinetics of thermal reactors based on the uranium fuel cycle, in which a fuel with a large concentration of uranium-238 is used (e.g., PWRs or BWRs). Most common reactor fuels are composed of either natural or partially enriched uranium. Typically, PWRs use an enriched uranium fuel (~4% of U-235) as a fresh fuel. Exposure to neutron flux gradually depletes the uranium-235, decreasing core reactivity (compensated by control rods, chemical shim, or burnable absorbers). The initial fuel load of a new reactor core (so-called first core) is entirely fresh fuel, fuel with no plutonium or fission products present. The contribution of uranium-238 directly to fission is quite small in most thermal reactors. On the other hand, uranium-238 plays a very important role, and this chapter is primarily about this isotope.
See also: Uranium
See also: Plutonium
http://www.oecd-nea.org/janis/
is a fissile isotope and its fission cross-section for thermal neutrons is about 585 barns (for 0.0253 eV neutron). For fast neutrons its fission cross-section is on the order of barns. Most of absorption reactions result in fission reaction, but a minority results in radiative capture forming 236U. The cross-section for radiative capture for thermal neutrons is about 99 barns (for 0.0253 eV neutron). Therefore about 15% of all absorption reactions result in radiative capture of neutron. About 85% of all absorption reactions result in fission.
Source: JANIS (Java-based nuclear information software)
http://www.oecd-nea.org/janis/
238U is a fissionable isotope but is not a fissile isotope. 238U cannot undergo a fission reaction after absorbing a thermal neutron. On the other hand, 238U can be fissioned by fast neutron with energy higher than >1MeV. During the fuel burning, the content of the U-235 continuously decreases, and the content of the plutonium increases (up to ~1% of Pu ). 238U also belongs to the group of fertile isotopes. Radiative capture of a neutron leads to the formation of fissile 239Pu and other transuranic elements. This is how 238U contributes to the operation of nuclear reactors and the production of electricity through this plutonium. For example, at a burnup of 40GWd/tU, about 40% of the total energy released comes from bred plutonium. This corresponds to a breeding ratio for this fuel burnup of about 0.4 to 0.5. That means about half of the fissile fuel in these reactors is bred there. This effect extends the cycle length for such fuels to sometimes nearly twice what it would otherwise be. MOX fuel has a smaller breeding effect than 235U fuel and is thus more challenging and slightly less economical to use due to a quicker drop-off in reactivity through cycle life.
http://www.oecd-nea.org/janis/
Plutonium 239 is a fissile isotope, and its fission cross-section for thermal neutrons is about 750 barns (for 0.025 eV neutron). For fast neutrons, its fission cross-section is on the order of barns. Most absorption reactions result in fission reactions, but a part of reactions result in radiative capture forming 240Pu. The cross-section for radiative capture for thermal neutrons is about 270 barns (for 0.025 eV neutron). Therefore about 27% of all absorption reactions result in radiative capture of incident neutron. About 73% of all absorption reactions result in fission.
http://www.oecd-nea.org/janis/
241Pu is a fissile isotope, which means 241Pu is capable of undergoing fission reaction after absorbing thermal neutron. Moreover 241Pu meets also alternative requirement that the amount of neutrons produced by fission of 241Pu (~2.94 per one fission by thermal neutron) is sufficient to sustain a nuclear fission chain reaction. Its fission cross-section for thermal neutrons is about 1012 barns (for 0.025 eV neutron). For fast neutrons its fission cross-section is on the order of barns. Most of absorption reactions result in fission reaction, but a part of reactions result in radiative capture forming 242Pu. The cross-section for radiative capture for thermal neutrons is about 363 barns (for 0.025 eV neutron). Therefore about 74% of all absorption reactions result in radiative capture of neutron. About 26% of all absorption reactions result in fission. 241Pu decays via beta decay into 241Am with half-life of only 14.3 years. 241Am has relatively high cross-section for radiative capture for thermal neutrons (~680 barns – 0.025eV). This two phenomena (decrease in fissile isotope and increase in neutron absorber) cause slight decrease in reactivity of irradiated fuel when stored in a spent fuel pool.
Evolution Equations
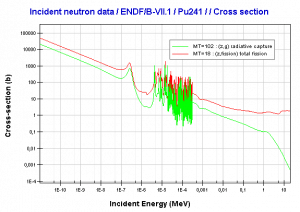
The exact evolution of isotopic changes is usually modeled mathematically by a set of differential equations known as evolution equations. These equations describe the rate of burnup of U-235, the rate of buildup of Pu-239, production of Pu-240 and Pu-241, the buildup of neutron-absorbing fission products and the overall rate of reactivity change in the reactor due to the changing composition of the fuel. The evolution equation can be constructed for each isotope. For example:
Special reference: W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
Special reference: Paul Reuss, Neutron Physics, EDP Sciences, 2008, ISBN: 2759800415.
Isotopic Changes – Summary
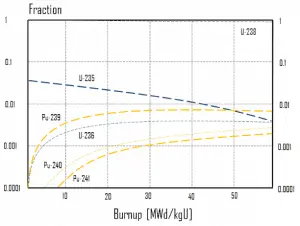
In summary, it can be seen for fuel burnup of 40 GWd/tU:
- Approximately 3 – 4% of the heavy nuclei are fissioned.
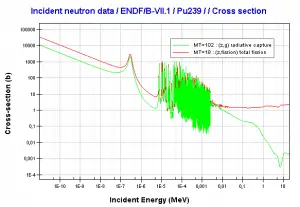
- About two-thirds of these fissions come directly from uranium 235, and the other third comes from plutonium produced from uranium 238. The contribution significantly increases as the fuel burnup increases.
- The removed fuel (spent nuclear fuel) still contains about 96% reusable material. It must be removed due to decreasing kinf of an assembly or, in other words, and it must be removed due to accumulation of fission products with significant absorption cross-section.
- Discharged fuel contains about 0.8% of plutonium and about 1% of uranium 235. It must be noted there is a significant content (about 0.5%) of uranium 236, which is neither a fissile isotope nor a fertile isotope.
Effect of Fuel Depletion on the Power Distribution
During the operation of a reactor, the amount of fissile material contained in the fuel assembly constantly decreases; therefore, the assembly kinf constantly decreases. During fuel depletion, the decrease of the assembly kinf will be greatest where the power is greatest. The differences in kinf between fresh fuel assemblies and high-burnup assemblies decreases. Therefore during cycle depletion, this process will cause the power to shift away from regions with the highest kinf. This process also depends on the use of burnable absorbers, which disrupt the first assumption about the constantly decreasing assembly kinf.
Effect of Fuel Depletion on Delayed Neutrons
In LWRs, the delayed neutron fraction decreases with fuel burnup. This is due to isotopic changes in the fuel. It is simple, and fresh uranium fuel contains only 235U as the fissile material, meanwhile during fuel burnup, the importance of fission of 239Pu increases (in some cases up to 50%). Since 239Pu produces significantly less delayed neutrons (0.0021 vs. 0.0064), the resultant core delayed neutron fraction of a multiplying system decreases (it is the weighted average of the constituent delayed neutron fractions). It follows then that the amount of reactivity insertion needed to produce a given reactor period decreases with the burnup of the fuel. This is also the reason why the neutron spectrum in the core becomes harder with fuel burnup.
βcore= ∑ Pi.βi
where Pi is fraction of power generated by isotope i.
Reactivity Effects of Fuel Burnup
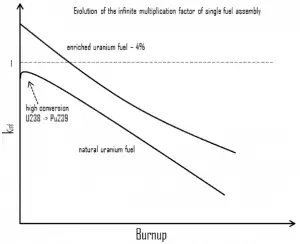↑burnup ⇒ ↓keff = ↓η .ε.p. ↓f . ↑↓Pf. ↑↓Pt
It is hard to describe the effects of fuel burnup on the six-factor formula, and it must be noted that criticality must be maintained for a long period. Therefore, all the negative effects must be compensated by increasing the thermal utilization factor (boron dilution or compensating rods withdrawal).
See more: Operational factors that affect the multiplication