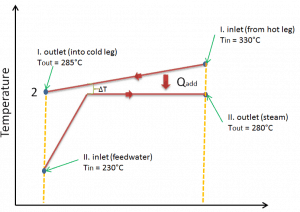
As was written, the interfacing variable is in pressurized water reactors the core inlet temperature, which is fully determined by steam pressure inside steam generators. Note that the core inlet temperature and the steam pressure are interconnected since heat (or power) transferred across a steam generator is:
q = h . ΔT
where:
- q is the amount of heat transferred (heat flux), W/m2, i.e., thermal power per unit area
- h is heat transfer coefficient, W/(m2.K)
- ΔT is the difference in temperature across the steam generator (in this case, the difference between the average temperature of the reactor coolant – Tavg and the saturation temperature determined by system pressure.
For all practical purposes, the heat transfer coefficient (h) is constant since the heat transfer coefficient is a function of the materials used in constructing the steam generator. The U-tubes are completely covered with water.
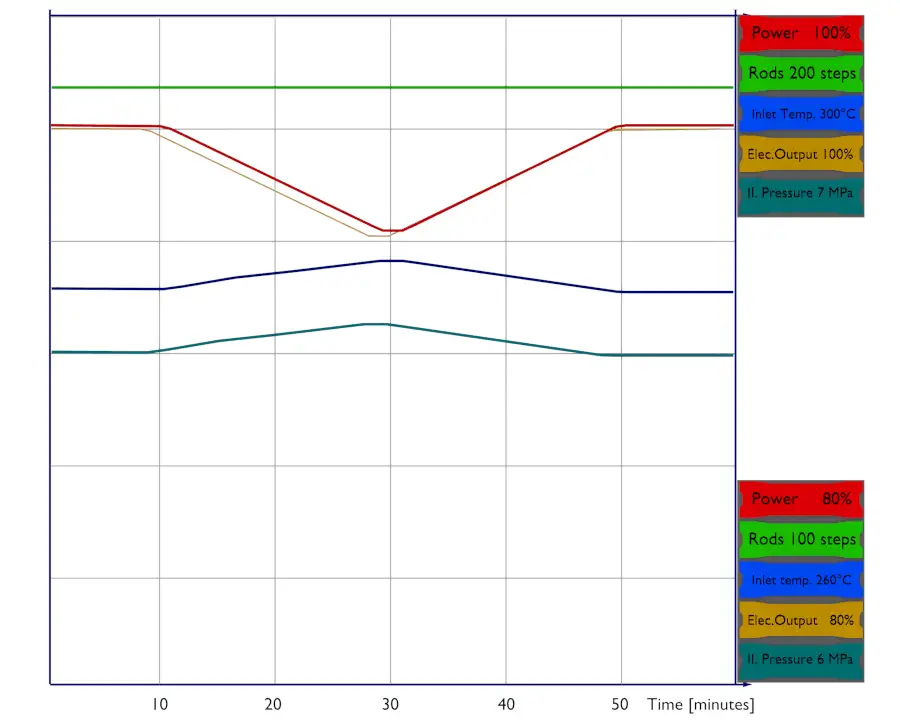
When a reactor is in automatic control, it follows the core inlet temperature – Tin(or the core average temperature – Tavg). Note that Tavg = (Tout + Tin) / 2. When there is a difference between actual Tin, actual and the temperature Tin, set, which is set in the system, the reactor control system initiates control rods movement. For example, when Tin, actual > Tin, set, the reactor control system automatically inserts control rods to decrease Tin, actual. The reactor thermal power remains constant because the rod’s movement only offsets the reactivity from the difference (Tin, actual – Tin, set) x MTC = moderator defect.
On the other hand, if the energy demand in the external system increases, more energy is removed from the reactor system, causing the temperature of the reactor coolant (Tin) to decrease. As the reactor coolant temperature decreases, positive reactivity is added, and a corresponding increase in reactor power level results. This reactor power increase occurs without any change in control rods position and without any change in boron concentration. The same inherent stability can be observed as the energy demand on the system is decreased.
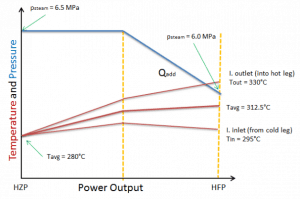
The core inlet temperature is directly given by system parameters in steam generators. When steam generators are operated at approximately 6.0MPa, it means the saturation temperature is equal to 275.6 °C. Since there must always be ΔT (~15°C) between the primary circuit and the secondary circuit, the reactor coolant (in the cold leg) have about 290.6°C (at HFP) at the inlet of the core. As the system pressure increases, the core inlet temperature must also increase, and this increase causes a slight increase in fuel temperature.
See also: Power Plant Control
The most significant effect of a variation in temperature upon reactor operation is the addition of positive or negative reactivity. As previously discussed, reactors are generally designed with negative temperature coefficients of reactivity (moderator and fuel temperature coefficients) as a self-limiting safety feature. A rise in reactor temperature results in the addition of negative reactivity. If the temperature rise is caused by an increase in reactor power, the negative reactivity addition slows and eventually turns the increase in reactor power. This is a highly desirable effect because it provides negative feedback in the event of an undesired power excursion.