Nuclear power plants rely on cooling systems to ensure the safe, continuous operation of the nuclear reactor. Cooling systems naturally ensure a heat transfer from a reactor core to steam generators, which is the main purpose of the cooling systems. Because of the large amount of heat generated in the reactor core by the fission reaction, the cooling systems demand a large volumetric flow of water (~80000 m3/hr) to ensure a sufficient and safe heat transfer. The cooling water is usually supplied by two or more large centrifugal pumps called reactor coolant pumps (RCPs). RCPs are not usually “safety systems”, as defined. After the loss of RCPs, the reactor must be shut down immediately. Sufficient and safe residual heat removal is then ensured by a natural circulation flow through the reactor. However, natural circulation is insufficient to remove the heat generated when the reactor is at power.
Reactor coolant pumps (RCPs) are used to pump primary coolant around the primary circuit. The purpose of the reactor coolant pump is to provide forced primary coolant flow to remove and transfer the amount of heat generated in the reactor core. There are many designs of these pumps, and there are many designs of primary coolant loops. There are significant differences between pumps for different reactor types. This article is focused on RCPs for pressurized water reactors. Most of PWRs use four RCPs in two or four loops design.
Generally, reactor coolant pumps are powerful, they can consume up to 6 MW each, and therefore, they can be used for heating the primary coolant before a reactor startup.
Reactor Cooling after Reactor Shutdown
Reactor Cooldown to Hot Standby Mode
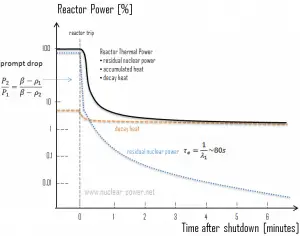In general, a reactor can be shut down for many reasons. Sometimes a reactor can be shut down only to Hot Standby mode, which means the operating temperature is normally maintained. Such a shutdown usually (e.g., a shutdown following a turbine trip) does not require the Reactor Coolant System (RCS) to be cooled down and depressurized. After a reactor is shut down, provisions are provided to remove decay heat. When the reactor coolant system (RCS) is at high pressure, the residual heat removal system (RHR) usually cannot be used for cooldown. In this case, decay heat is removed through the secondary system. For RCS cooldown (to Hot Standby mode), steam generators usually dissipate heat directly to the main condenser or the atmospheric steam dump system. Some reactor coolant pumps (RCPs) must be in operation in this operational mode. Proper loop flow and desired loop temperatures are maintained with these RCPs until the residual heat removal system (RHRS) is in service. If the plant remains in this condition for some time, SDM must be maintained (including xenon transients) by changes in boron concentration.
Reactor Cooldown to Cold Shutdown Mode
If the shutdown period will be lengthy or involves functions requiring the cooldown of the reactor (e.g., shutdown for refueling), the system temperature and pressure can be lowered by many methods. The methods for conducting the reactor’s cooldown vary depending on plant design. Still, in all cases, limitations are imposed on the maximum rate at which the reactor systems may be cooled. These limits are provided to reduce the stress applied to system materials, reducing the possibility of stress-induced failure. During this cooldown, the system pressure decreases as steam generator steam pressure decreases. SDM must also be maintained in this case. Therefore, boration is initiated to bring the boron concentration to the cold shutdown value. Reactor coolant pumps are run only as needed to assure uniform loops and reactor pressure vessel cooldown and provide spray for pressurizer cooldown.
When the RCS pressure is lower than the residual heat removal (RHR) system design pressure, this system is used for further cooldowns, depressurization, and long-term reactor cooling. The RHR system in PWRs takes water from one or two RCS hot legs, cools it in RHR heat exchangers, and pumps it back to the cold legs or core flooding tank nozzles. To accomplish RHR heat removal, RHR heat exchangers transfer heat to the component cooling water or service water system, which then transports heat to the ultimate heat sink (UHS).
The time required for plant cooldown is approximately 10 to 20 hours, which corresponds to a cooldown rate of 15 to 30°C per hour. The final conditions are – the NSSS – Nuclear Steam Supply System is in the “cold shutdown” mode, that means Tavg = 30°C, pressure = near atmospheric, boron concentration is sufficient to yield 2 to 5% shutdown margin and RCPs – Reactor Coolant Pumps are off. Prior to each point of the procedure above, compliance with the plant Technical Specifications must be verified.
See also: Decay Heat
