The process of reaching criticality (i.e., keff = 1) is known as the criticality approach or startup to minimum load. Prior to this process, the boron concentration is usually sufficient (after refueling) to yield ~10% shutdown margin (i.e., keff = 0,90), the control rods are fully inserted into the core. If allowed, the boron concentration can be adjusted to the required value prior to startup.
For the criticality approach, parameters known as estimated critical conditions must be known. Estimated critical conditions are precalculated for each fuel loading pattern and usually consist from:
- Estimated critical rod position (e.g., the last control rod bank at 90% of the core height)
- Estimated critical boron concentration (e.g., cB = 9 g/kg = 1573 ppm)
- Estimated critical core inlet temperature (e.g., Tin = 275°C)
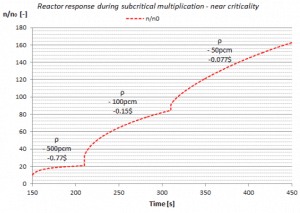
These three parameters together specifies the estimated critical state. The control rods must satisfy the requirement known as the rod insertion limit, and the rod insertion limit ensures shutdown margin requirements. There are many ways how to reach a critical state, but usually, the following two procedures are used:
- Approach by control rods withdrawal. When the existing boron concentration is near the estimated critical, the approach can be performed only by control rods withdrawal. Sometimes the boron concentration can be adjusted to the required value prior to startup, and then this procedure can be used. The control rods are withdrawn from the core in successive steps. The shutdown rod banks are withdrawn in sequence, and then the control banks are withdrawn manually to achieve criticality. Following each step, the neutron count rate is registered. Experimentally the neutron count rate is measured by source range neutron detectors (usually three in the 120° symmetry) located at different positions outside the reactor. The neutron level following each addition of reactivity should be allowed to stabilize to obtain an accurate indication of asymptotic multiplication before proceeding with the next reactivity addition. This stabilization time becomes progressively larger as criticality is approached.
- Approach by boron dilution. When the existing boron concentration is far from the estimated critical, and the adjustment is not allowed, the critical state must be approached by boron dilution. Prior to boron dilution, the shutdown and control rods are withdrawn to estimated critical condition (e.g., all at ARO position except the last control rod bank, which is withdrawn to 90% of the core height). Then the boron concentration can be lowered by introducing condensate into the reactor coolant system. This process is not performed by steps. Therefore, there is no stabilization to obtain an accurate indication of asymptotic multiplication. Also, in this case, the neutron count rate is measured by source range neutron detectors.
See also: Subcritical Multiplication
Evidence of criticality is indicated by a positive, sustained startup rate or by reactimeter with no rod motion and increasing source range counts. After criticality is achieved, a positive startup rate is established (reactor is slightly supercritical), and the power level increases up to “minimum load”. This power increase is then stabilized at minimum load by control rods insertion. At minimum load, the power level does not influence the criticality (keff) of a power reactor unless thermal reactivity feedbacks act (operation of a power reactor without reactivity feedbacks is between 10E-8% – 1% of rated power). The reactor behaves as a “zero power reactor”.
It is very important to pay attention to safety instructions. Since the reactor is at low power, the reactor is far from temperature feedback, improving reactor stability. There is a possibility that automatic shutdown, which can be activated by a reactor protection system in case too much reactivity is inserted.
The inherent power stability is ineffective below the point known as the “point of adding heat”. Suppose a power excursion is initiated from a very low power level. In that case, power will continue to rise unchecked until the point of adding heat is reached, and the subsequent temperature rise adds negative reactivity to slow the rise of reactor power.
See also: 1/M Plot
See also: Source Neutrons