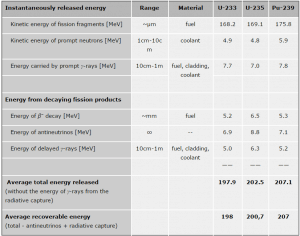
In a nuclear reactor, the average recoverable energy per fission is about 200 MeV, being the total energy minus the energy of the energy of antineutrinos that are radiated away. About 6 percent of the 200 MeV produced by average fission is released with the delay at some time after the instant of fission. This energy comes from the beta and gamma decay of fission products and transuranic elements accumulated in the fuel rather than directly from the fission process itself. Most of these fission products are highly unstable (radioactive) and undergo further radioactive decays to stabilize themselves. On average, after each U-235 fission, the neutron-rich fission fragments must undergo 6 negative beta decays (6 neutrons must decay to 6 protons). Absorption of this radiation in the fuel generates a significant amount of heat even when a reactor is shut down.
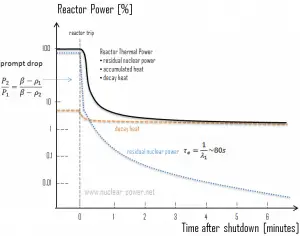 When a reactor is shut down, fission essentially ceases, but decay energy is still being produced. The energy produced after shutdown is referred to as decay heat. The amount of decay heat production after shutdown is directly influenced by the reactor’s power history (fission products accumulation) prior to shutdown and by the level of fuel burnup (actinides accumulation – especially in case of spent fuel handling). A reactor operated at full power for 10 days prior to the shutdown has much higher decay heat generation than a reactor operated at low power for the same period. On the other hand, when the reactor changes its power from 50% to 100% of full power, the ratio of decay heat to neutron power drops to roughly half its previous level. It then builds up slowly as the fission product inventory adjusts to the new power.
When a reactor is shut down, fission essentially ceases, but decay energy is still being produced. The energy produced after shutdown is referred to as decay heat. The amount of decay heat production after shutdown is directly influenced by the reactor’s power history (fission products accumulation) prior to shutdown and by the level of fuel burnup (actinides accumulation – especially in case of spent fuel handling). A reactor operated at full power for 10 days prior to the shutdown has much higher decay heat generation than a reactor operated at low power for the same period. On the other hand, when the reactor changes its power from 50% to 100% of full power, the ratio of decay heat to neutron power drops to roughly half its previous level. It then builds up slowly as the fission product inventory adjusts to the new power.
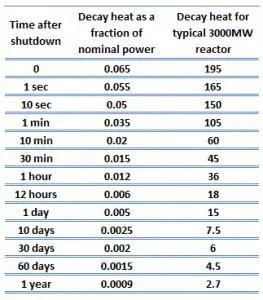 The decay heat produced after a reactor shutdown from full power is initially equivalent to 6 to 7% of the rated thermal power. Since radioactive decay is a random process at the level of single atoms, it is governed by the radioactive decay law. Note that irradiated nuclear fuel contains many different isotopes that contribute to decay heat, all subject to the radioactive decay law. Therefore a model describing decay heat must consider decay heat to be a sum of exponential functions with different decay constants and initial contribution to the heat rate. Fission fragments with a short half-life are much more radioactive (at the time of production) and contribute significantly to decay heat but will lose their share rapidly. On the other hand, fission fragments and transuranic elements with a long half-life are less radioactive (at the time of production) and produce less decay heat but will lose their share more slowly. This decay heat generation rate diminishes to about 1% approximately one hour after shutdown. The decay comes from the beta and gamma decay of fission products and transuranic elements (+ alpha decay).
The decay heat produced after a reactor shutdown from full power is initially equivalent to 6 to 7% of the rated thermal power. Since radioactive decay is a random process at the level of single atoms, it is governed by the radioactive decay law. Note that irradiated nuclear fuel contains many different isotopes that contribute to decay heat, all subject to the radioactive decay law. Therefore a model describing decay heat must consider decay heat to be a sum of exponential functions with different decay constants and initial contribution to the heat rate. Fission fragments with a short half-life are much more radioactive (at the time of production) and contribute significantly to decay heat but will lose their share rapidly. On the other hand, fission fragments and transuranic elements with a long half-life are less radioactive (at the time of production) and produce less decay heat but will lose their share more slowly. This decay heat generation rate diminishes to about 1% approximately one hour after shutdown. The decay comes from the beta and gamma decay of fission products and transuranic elements (+ alpha decay).
- The energy of delayed β– decay. About 6 MeV of fission energy is in the form of the kinetic energy of electrons (beta particles). The fission fragments are neutron-rich nuclei, and therefore they usually undergo beta decay to stabilize themselves. Beta particles deposit their energy essentially in the fuel element, within about 1 mm of the fission fragment.
- The energy of delayed gamma decay. Gamma rays usually accompany beta decay, and the gamma rays are well attenuated by high-density and high Z materials. In a reactor core, the largest share of the energy will be deposited in the fuel containing uranium dioxide. Still, a significant share of the energy will also be deposited in the fuel cladding and the coolant (moderator). The range of gamma rays in a reactor varies according to the initial energy of the gamma-ray. It can be stated that most gammas in a reactor have ranged from 10cm – 1m.
Classification according to the source material:
- Decay of fission products. Decay of fission products dominates source directly after shutdown and in periods up to years.
- Decay of actinides produced by radiative capture (especially 239Pu). Decay of 239Pu and 240Pu is the dominating source from the long-term point of view (e.g., units or up to tens of years after shutdown – depending on the fuel burnup). 239Pu itself decays via alpha decay into 235U with a half-life of 24 100 years. It significantly depends on the fuel burnup, and it determines conditions for spent fuel handling. (See also: Fuel Depletion)
- Decay of activated structural materials by radiative capture. Decay of activated structural materials is a minor contributor to overall decay heat.
See also: ANSI/ANS-5.1-2014, Decay Heat Power in Light Water Reactors. American Nuclear Society, 2014.
However, even at these low levels (about 1% after one hour), the amount of heat generated requires the continued removal of heat for an appreciable time after shutdown. Decay heat is a long-term consideration and impacts spent fuel handling, reprocessing, waste management, and reactor safety.
The reactor’s design must allow for the removal of this decay heat from the core by some means. If adequate heat removal is not available, decay heat will increase the temperatures in the core to the point that fuel melting and core damage will occur, as in the case of Three Mile Island and Fukushima. The degree of concern with decay heat will vary according to reactor type and design. Therefore, there is little concern about core temperature due to decay heat for low power, pool-type reactors.
Decay Heat Removal
Methods for removing decay or residual heat from a reactor core can be grouped into two general categories:
- Closed-Loop System. One category includes methods that circulate fluid through the reactor core in a closed-loop, using some type of heat exchanger to transfer heat out of the system.
- Heat Removal through Steam Generators. Steam generators can be used to remove decay heat from a reactor, and they dissipate heat directly to the main condenser or the atmospheric steam dump system. In this operational mode, some reactor coolant pumps (RCPs) must usually be in operation, or natural circulation must have remained.
- Heat Removal through RHR. The residual heat removal system (RHR) is a low-pressure heat removal system. PWRs take water from one or two RCS hot legs, cool it in RHR heat exchangers, and pump it back to the cold legs or core flooding tank nozzles. To accomplish RHR heat removal, RHR heat exchangers transfer heat to the component cooling water or service water system, which then transports heat to the ultimate heat sink (UHS).
- Open System: The other category includes methods that operate in an open system, drawing in cool fluid from some source and discharging warmer fluid to some storage area or the environment.
- Decay heat removal using the feed-and-bleed method. The feed-and-bleed method for decay heat removal becomes a necessary method in some pressurized water reactors (PWRs) if there is a loss of steam generator heat sink capability. The feed-and-bleed technique involves passing hot coolant out of the primary system through a pilot-operated relief valve (PORV) while simultaneously feeding the primary system with subcooled coolant through a high-pressure safety injection system (HPSI), which is part of the emergency core cooling system.
Calculation of Decay Heat – Wigner-Way formula
The amount of decay heat being generated in a fuel assembly at any time after shutdown can be exactly calculated by the determination of the number of fission products present at the time of shutdown. This is a fairly detailed process and is dependent upon power history. The concentrations, decay energies, and half-lives of fission products are known for a given type of fuel. By starting from a known value, based on power history at shutdown, the decay heat generation rate can be calculated for any time after shutdown. An exact solution must consider the fact that hundreds of different radionuclides are present in the core, each with its concentration and decay half-life. For this purpose, the SCALE/TRITON code can be used for depletion calculations. The SCALE/ORIGEN-ARP code can be used to calculate decay heat rates at specific initial fuel composition and discharge burnup levels.
See also: Brian J. Ade, Ian C. Gauld. Decay Heat Calculations for PWR and BWR Assemblies Fueled with Uranium and Plutonium Mixed Oxide Fuel Using Scale, ORNL/TM-2011/290, OAK RIDGE NATIONAL LABORATORY, 2011.
It is also possible to make a rough approximation by using a single half-life that represents the overall decay of the core over a certain period. An equation that uses this approximation is the Wigner-Way formula:
where
- Pd(t) = thermal power generation due to beta and gamma rays,
- P0 = thermal power before the shutdown,
- t0 = time, in seconds, of thermal power level before the shutdown,
- t = time, in seconds, elapsed since the shutdown.