Article Summary & FAQs
What is nuclear energy?
By definition, nuclear energy refers to the combined potential energy that binds nucleons to form the atomic nucleus. The nuclear particles are bound together by the strong nuclear force. Weak nuclear forces provide the potential energy for certain kinds of radioactive decay.
- Separate nucleons contain a huge amount of nuclear potential energy. In terms of energy, they rather bind together to form compound nuclei, and during their formation, this potential energy is released. That is what we call nuclear energy.
- Nuclear energy comes either from spontaneous nuclei conversions or induced nuclei conversions. It is associated with nuclear binding power. When nuclear energy is generated (splitting atoms, nuclear fusion, or nuclear reactions), a small amount of mass (saved in the nuclear binding energy) transforms into pure energy (such as kinetic energy, thermal energy, or radiant energy).
- In general, nuclear fission and nuclear fusion result in the release of enormous quantities of nuclear energy because the binding energy stored in atomic nuclei is very high.
- The amount of nuclear energy released is so high that you can measure a decrease in the mass of products.
- One of the striking results of Einstein’s theory of relativity is that mass and energy are equivalent and convertible, one into the other. E = mc2
- In 2011 nuclear power provided 10% of the world’s electricity. In 2007, the IAEA reported 439 nuclear power reactors operating globally, operating in 31 countries.
What is Nuclear Energy
By definition, nuclear energy refers to the combined potential energy that binds nucleons to form the atomic nucleus. The nuclear particles are bound together by the strong nuclear force. Weak nuclear forces provide the potential energy for certain kinds of radioactive decay.
Nuclear energy comes either from spontaneous nuclei conversions or induced nuclei conversions. Among these conversions (nuclear reactions) are nuclear fission, nuclear decay, and nuclear fusion. Conversions are associated with mass and energy changes. One of the striking results of Einstein’s theory of relativity is that mass and energy are equivalent and convertible, one into the other. Einstein’s famous formula describes equivalence of the mass and energy:
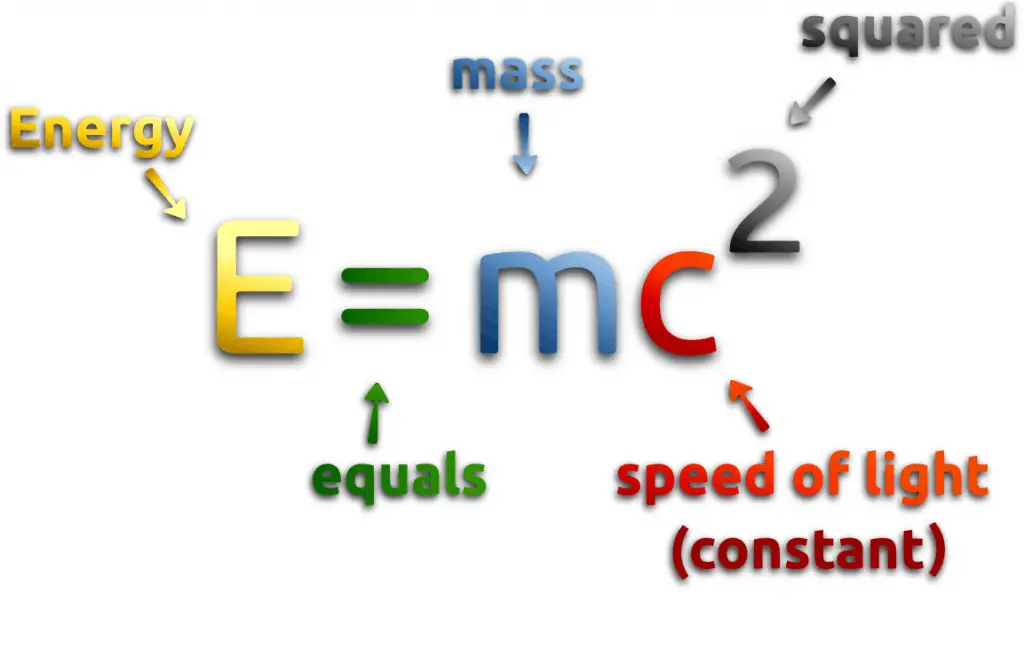
Where M is the small amount of mass and C is the speed of light.
What does that mean? If nuclear energy is generated (splitting atoms, nuclear fusion), a small amount of mass (saved in the nuclear binding energy) transforms into pure energy (such as kinetic energy, thermal energy, or radiant energy).
The energy equivalent of one gram (1/1000 of a kilogram) of mass is equivalent to:
- 89.9 terajoules
- 25.0 million kilowatt-hours (≈ 25 GW·h)
- 21.5 billion kilocalories (≈ 21 Kcal)
- 85.2 billion BTUs
or to the energy released by combustion of the following:
- 21.5 kilotons of TNT-equivalent energy (≈ 21 kt)
- 568,000 US gallons of automotive gasoline
Whenever energy is generated, the process can be evaluated in terms of E = mc2.
Q-value – Energetics of Nuclear Reactions
In nuclear and particle physics the energetics of nuclear reactions is determined by the Q-value of that reaction. The Q-value of the reaction is defined as the difference between the sum of the masses of the initial reactants and the sum of the masses of the final products, in energy units (usually in MeV).
For reactions in which there is an increase in the kinetic energy of the products Q is positive. The positive Q reactions are said to be exothermic (or exergic). There is a net release of energy, since the kinetic energy of the final state is greater than the kinetic energy of the initial state.
For reactions in which there is a decrease in the kinetic energy of the products Q is negative. The negative Q reactions are said to be endothermic (or endoergic) and they require a net energy input.
See also: Q-value
Nuclear Binding Energy – Mass Defect
In the special theory of relativity, certain types of matter may be created or destroyed. Still, the mass and energy associated with such matter remain unchanged in quantity in all of these processes. Mass was no longer considered unchangeable in the closed system. It was found the rest mass of an atomic nucleus is measurably more minor than the sum of the rest masses of its constituent protons, neutrons, and electrons. The difference is a measure of the nuclear binding energy which holds the nucleus together. According to the Einstein relationship (E = mc2), this binding energy is proportional to this mass difference, known as the mass defect.
At the nuclear level, the nuclear binding energy is the energy required to disassemble (to overcome the strong nuclear force) a nucleus of an atom into its component parts (protons and neutrons).
During the nuclear splitting or nuclear fusion, some of the mass of the nucleus gets converted into huge amounts of energy. Thus this mass is removed from the total mass of the original particles, and the mass is missing in the resulting nucleus. The nuclear binding energies are enormous. They are on the order of a million times greater than the electron binding energies of atoms.
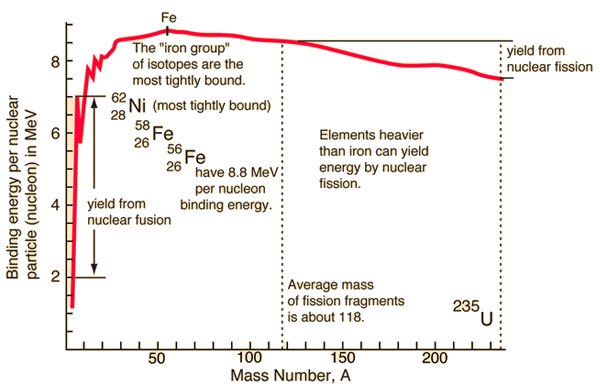
Source: hyperphysics.phy-astr.gsu.edu
If the splitting releases energy and the fusion release the energy, so where is the breaking point? For understanding this issue, it is better to relate the binding energy to one nucleon to obtain a nuclear binding curve. The binding energy per one nucleon is not linear. There is a peak in the binding energy curve in the region of stability near iron. Either the breakup of heavier nuclei than iron or lighter nuclei than iron will yield energy.
The reason the trend reverses after the iron peak is the growing positive charge of the nuclei. The electric force has a more extended range than the strong nuclear force. While the strong nuclear force binds only close neighbors, the electric force of each proton repels the other protons.
Example: Nuclear Energy Release in Nuclear Fission
From the nuclear binding energy curve and from the table, it can be seen that, in the case of splitting a 235U nucleus into two parts, the binding energy of the fragments (A ≈ 120) together is more significant than that of the original 235U nucleus.
According to the Weizsaecker formula, the total energy released for such a reaction will be approximately 235 x (8.5 – 7.6) ≈ 200 MeV.
Example: Mass defect of a 63Cu
Calculate the mass defect of a 63Cu nucleus if the actual mass of 63Cu in its nuclear ground state is 62.91367 u.
63Cu nucleus has 29 protons and also has (63 – 29) 34 neutrons.
The mass of a proton is 1.00728 u, and a neutron is 1.00867 u.
The combined mass is: 29 protons x (1.00728 u/proton) + 34 neutrons x (1.00867 u/neutron) = 63.50590 u
The mass defect is Δm = 63.50590 u – 62.91367 u = 0.59223 u
Convert the mass defect into energy (nuclear binding energy).
(0.59223 u/nucleus) x (1.6606 x 10-27 kg/u) = 9.8346 x 10-28 kg/nucleus
ΔE = (9.8346 x 10-28 kg/nucleus) x (2.9979 x 108 m/s)2 = 8.8387 x 10-11 J/nucleus
The energy calculated in the previous example is nuclear binding energy. However, the nuclear binding energy may be expressed as kJ/mol (for better understanding).
Calculate the nuclear binding energy of 1 mole of 63Cu:
(8.8387 x 10-11 J/nucleus) x (1 kJ/1000 J) x (6.022 x 1023 nuclei/mol) = 5.3227 x 1010 kJ/mol of nuclei.
One mole of 63Cu (~63 grams) is bound by the nuclear binding energy (5.3227 x 1010 kJ/mol), which is equivalent to:
- 14.8 million kilowatt-hours (≈ 15 GW·h)
- 336,100 US gallons of automotive gasoline
Example: Mass defect of the reactor core
Calculate the mass defect of the 3000MWth reactor core after one year of operation.
It is known as the average recoverable energy for fission is about 200 MeV, which is the total energy minus the energy of the antineutrinos that are radiated away.
The reaction rate per entire 3000MWth reactor core is about 9.33×1019 fissions/second.
The overall energy release in the units of joules is:
200×106 (eV) x 1.602×10-19 (J/eV) x 9.33×1019 (s-1) x 31.5×106 (seconds in year) = 9.4×1016 J/year
The mass defect is calculated as:
Δm = ΔE/c2
Δm = 9.4×1016 / (2.9979 x 108)2 = 1.046 kg
That means in a typical 3000MWth reactor core, about 1 kilogram of the matter is converted into pure energy.
Note that a typical annual uranium load for a 3000MWth reactor core is about 20 tons of enriched uranium (i.e., about 22.7 tons of UO2). The entire reactor core may contain about 80 tonnes of enriched uranium.
Mass defect directly from E=mc2
The mass defect can be calculated directly from the Einstein relationship (E = mc2) as:
Δm = ΔE/c2
Δm = 3000×106 (W = J/s) x 31.5×106 (seconds in year) / (2.9979 x 108)2 = 1.051 kg
Nuclear Energy and Electricity Production
Today we use nuclear energy to generate proper heat and electricity. This electricity is generated in nuclear power plants. The heat source in the nuclear power plant is a nuclear reactor. As is typical in all conventional thermal power stations, the heat is used to generate steam which drives a steam turbine connected to a generator that produces electricity. In 2011 nuclear power provided 10% of the world’s electricity. In 2007, the IAEA reported 439 nuclear power reactors operating in the world, operating in 31 countries. They produce base-load electricity 24/7 without emitting any pollutants into the atmosphere (this includes CO2).
Nuclear Energy Consumption – Summary

Consumption of a 3000MWth (~1000MWe) reactor (12-months fuel cycle)
It is an illustrative example, and the following data do not correspond to any reactor design.
- A typical reactor may contain about 165 tonnes of fuel (including structural material)
- A typical reactor may contain about 100 tonnes of enriched uranium (i.e., about 113 tonnes of uranium dioxide).
- This fuel is loaded, for example, into 157 fuel assemblies composed of more than 45,000 fuel rods.
- A typical fuel assembly contains energy for approximately four years of operation at full power.
- Therefore about one-quarter of the core is yearly removed to the spent fuel pool (i.e., about 40 fuel assemblies). At the same time, the remainder is rearranged to a location in the core better suited to its remaining level of enrichment (see Power Distribution).
- The removed fuel (spent nuclear fuel) still contains about 96% of reusable material (it must be removed due to decreasing kinf of an assembly).
- This reactor’s annual natural uranium consumption is about 250 tons of natural uranium (to produce about 25 tonnes of enriched uranium).
- The annual enriched uranium consumption of this reactor is about 25 tonnes of enriched uranium.
- The annual fissile material consumption of this reactor is about 1 005 kg.
- The annual matter consumption of this reactor is about 1.051 kg.
- But it corresponds to about 3 200 000 tons of coal burned in coal-fired power plants per year.
See also: Fuel Consumption