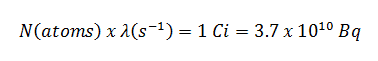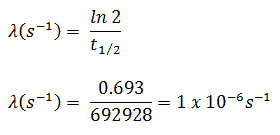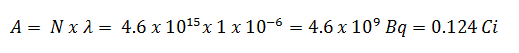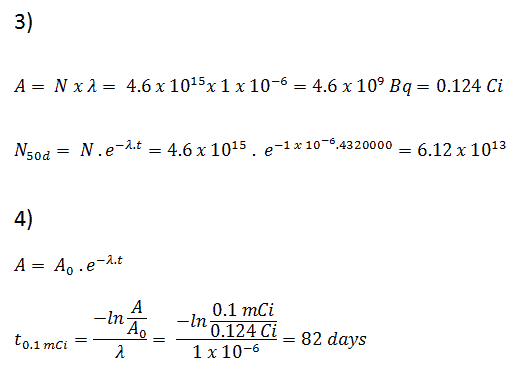Article Summary & FAQs
What is radioactive decay?
Radioactive decay, also known as nuclear decay or radioactivity, is a random process by which an unstable atomic nucleus loses its energy by emission of radiation or particle. A material containing unstable nuclei is considered radioactive.
Key Facts
- There are only certain combinations of neutrons and protons, which form stable nuclei. As the number of protons increases, an increasing ratio of neutrons to protons is needed to form a stable nucleus. If there are too many (neutrons also obey the Pauli exclusion principle) or too few neutrons for a given number of protons, the resulting nucleus is not stable, and it undergoes radioactive decay.
- Radioactive decay is a random process at the level of single atoms, in that, according to quantum theory, it is impossible to predict when a particular atom will decay. In other words, a nucleus of a radionuclide has no “memory”.
- There are three basic modes of radioactive decay:
- Alpha decay.Beta-decay.
- Gamma decay.
Additional important decay modes:
- A measure of radioactivity (activity) is based on the counting of disintegrations per second. The SI unit of activity is the becquerel (Bq), equal to one reciprocal second.
- The radioactive decay of a certain number of atoms (mass) is exponential in time. Radioactive decay law: N = N.e-λt The rate of nuclear decay is also measured in terms of half-lives. Radioactive material with a short half-life is much more radioactive (at the time of production) but will obviously lose its radioactivity rapidly.
- In physics, a radioactive decay chain is a sequence of unstable atomic nuclei and their modes of decays, which leads to a stable nucleus.
- Radioactivity is a natural process by which unstable nuclei stabilize themselves. In small amounts, radioactivity is all around us. In, around, and above the world we live in. It is a natural energy force that surrounds us. It is a part of our natural world that has been here since the birth of our planet. From the beginning of time, all living creatures have been, and are still being, exposed to ionizing radiation, which is produced by natural radioactive sources.
- The decay heat of uranium and thorium and their decay products (e.g.,, radon, radium, etc.) contribute to heating the Earth’s core. Together with potassium-40 in the Earth’s mantle, these elements are the main source of heat that keeps the Earth’s core liquid.
What is Radioactive Decay
Nuclear decay (Radioactive decay) occurs when an unstable atom loses energy by emitting ionizing radiation. Radioactive decay is a random process at the level of single atoms, in that, according to quantum theory, it is impossible to predict when a particular atom will decay. In other words, a nucleus of a radionuclide has no “memory”. A nucleus does not “age” over time. Thus, the probability of its breaking down does not increase with time but stays constant no matter how long the nucleus has existed. During its unpredictable decay, this unstable nucleus spontaneously and randomly decomposes to form a different nucleus (or a different energy state – gamma decay), giving off radiation in the form of atomic particles or high energy rays. This decay occurs at a constant, predictable rate that is referred to as half-life. A stable nucleus will not undergo this kind of decay and is thus non-radioactive.
Source: chemwiki.ucdavis.edu
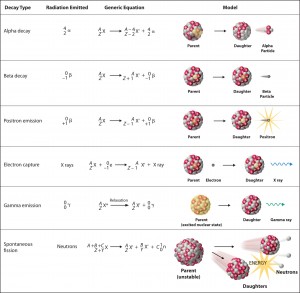
There are three basic modes of radioactive decay:
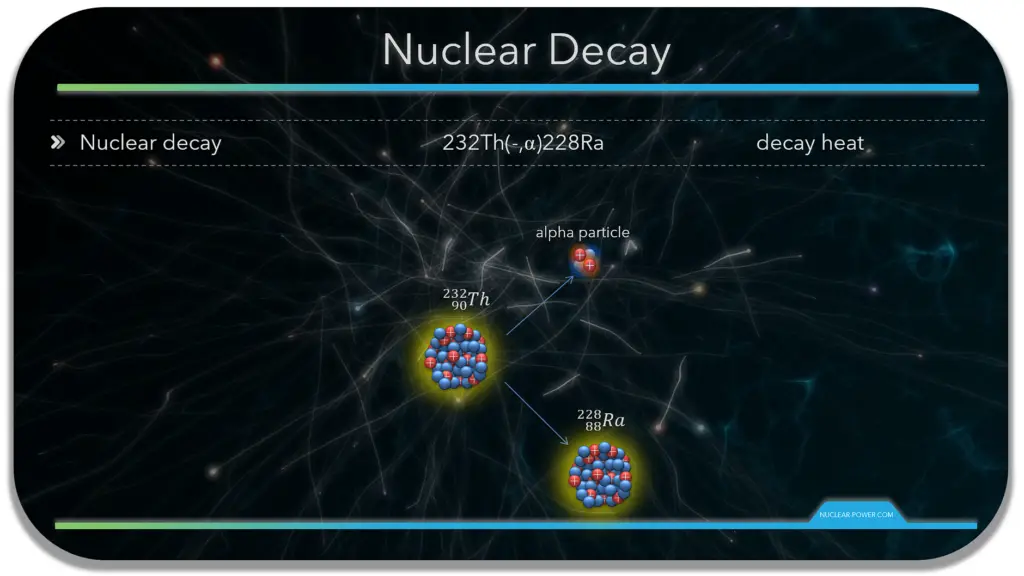
- Alpha decay. Alpha decay represents the disintegration of a parent nucleus to a daughter through the emission of the nucleus of a helium atom. Alpha particles consist of two protons and two neutrons bound together into a particle identical to a helium nucleus. Because of its very large mass (more than 7000 times the mass of the beta particle) and its charge, it heavily ionizes material and has a very short range.
- Beta-decay. Beta-decay or β decay represents the disintegration of a parent nucleus to a daughter through the emission of the beta particle. Beta particles are high-energy, high-speed electrons or positrons emitted by certain radioactive nuclei such as potassium-40. The beta particles have a greater range of penetration than alpha particles but still much less than gamma rays. The beta particles emitted are a form of ionizing radiation, also known as beta rays. The production of beta particles is termed beta decay.
- Gamma decay. Gamma decay or γ decay represents the disintegration of a parent nucleus to a daughter through the emission of gamma rays (high energy photons). Gamma rays are electromagnetic radiation (high energy photons) of a very high frequency and high energy. Nuclei decay produces them as they transition from a high-energy state to a lower state known as gamma decay. Gamma emissions accompany most nuclear reactions.
Additional important decay modes:
- Electron capture. Electron capture is when a parent nucleus captures one of its orbital electrons and emits a neutrino. Electron capture, also known as inverse beta decay, is sometimes included as a type of beta decay because the basic nuclear process, mediated by the weak interaction, is the same.
- Internal conversion. Internal conversion is an electromagnetic process by which a nuclear excited state decays by the direct emission of one of its atomic electrons. Internal conversion competes with gamma emission, but in this case, the electromagnetic multipole fields of the nucleus do not result in the emission of a gamma-ray. Instead, the fields interact directly with atomic electrons. In contrast to beta decay, governed by a weak force, the electron is emitted from the radioactive atom but not from the nucleus.
- Neutron decay. Neutron decay is a type of radioactive decay of nuclei containing excess neutrons (especially fission products), in which a neutron is simply ejected from the nucleus. This type of radiation plays a key role in nuclear reactor control because these neutrons are delayed neutrons.
- Proton decay. Proton decay is a rare type of radioactive decay of nuclei containing excess protons, in which a proton is simply ejected from the nucleus.
- Spontaneous fission. Spontaneous fission (SF) is a form of radioactive decay found only in very heavy chemical elements.
Nature of Decay
As was written, atomic nuclei consist of protons and neutrons, which attract each other through nuclear force. In contrast, protons repel each other via electromagnetic force due to their positive charge. These two forces compete, leading to various stability of nuclei. There are only certain combinations of neutrons and protons, which form stable nuclei. Neutrons stabilize the nucleus because they attract each other and protons, which helps offset the electrical repulsion between protons. As a result, as the number of protons increases, an increasing ratio of neutrons to protons is needed to form a stable nucleus. If there are too many (neutrons also obey the Pauli exclusion principle) or too few neutrons for a given number of protons, the resulting nucleus is not stable, and it undergoes radioactive decay. Most atoms found in nature are stable and do not emit particles or energy that change over time. Of the first 82 elements in the periodic table, 80 have isotopes considered to be stable. Technetium, promethium, and elements with an atomic number over 82 are unstable and decompose through radioactive decay. Unstable isotopes decay spontaneously through various radioactive decay pathways, most commonly alpha decay, beta decay, gamma decay, or electron capture. Many other rare types of decay, such as spontaneous fission or neutron emission, are known.
Conservation Laws in Nuclear Decay
In analyzing nuclear reactions, we apply the many conservation laws. Nuclear reactions are subject to classical conservation laws for a charge, momentum, angular momentum, and energy (including rest energies). Additional conservation laws, not anticipated by classical physics, are:
- Law of Conservation of Lepton Number
- Law of Conservation of Baryon Number
- Law of Conservation of Electric Charge
Certain of these laws are obeyed under all circumstances. Others are not. We have accepted the conservation of energy and momentum. In all the examples given, we assume that the number of protons and the number of neutrons is separately conserved. We shall find circumstances and conditions in which this rule is not true. Where we are considering non-relativistic nuclear reactions, it is essentially true. However, where we consider relativistic nuclear energies or those involving weak interactions, we shall find that these principles must be extended.
Some conservation principles have arisen from theoretical considerations. Others are just empirical relationships. Notwithstanding, any reaction not expressly forbidden by the conservation laws will generally occur, if perhaps at a slow rate. This expectation is based on quantum mechanics. Unless the barrier between the initial and final states is infinitely high, there is always a non-zero probability that a system will make the transition between them.
To analyze non-relativistic reactions, it is sufficient to note four of the fundamental laws governing these reactions.
- Conservation of nucleons. The total number of nucleons before and after a reaction are the same.
- Conservation of charge. The sum of the charges on all the particles before and after a reaction are the same.
- Conservation of momentum. The total momentum of the interacting particles before and after a reaction is the same.
- Conservation of energy. Energy, including rest mass energy, is conserved in nuclear reactions.
Reference: Lamarsh, John R. Introduction to Nuclear engineering 2nd Edition
Activity – Specific Activity
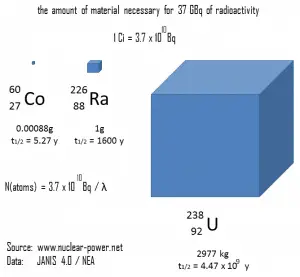A measure of radioactivity (activity) is based on the counting of disintegrations per second. The SI unit of activity is the becquerel (Bq), equal to one reciprocal second. The activity depends only on the number of decays per second, not on the type of decay, the energy of the decay products, or the biological effects of the radiation. It can be used to characterize the rate of emission of ionizing radiation. Specific activity is the activity per quantity of a radionuclide. Thus specific activity is defined as the activity per quantity of atoms of a particular radionuclide. It is usually given in units of Bq/g, but another commonly used unit of activity is the curie (Ci), allowing the definition of specific activity in Ci/g.
Units of activity (the curie and the becquerel) can also be used to characterize an overall quantity of controlled or accidental releases of radioactive atoms.
Units of Activity
- Becquerel. The becquerel is the SI unit of radioactivity defined in 1974. It is named in honor of Henri Becquerel, a French physicist who discovered radioactivity in 1896. One becquerel (1Bq) is equal to 1 disintegration per second.
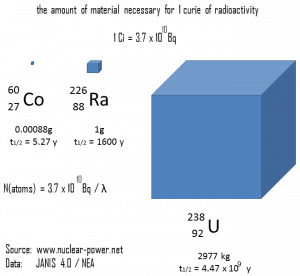
- Curie. The curie is a non-SI unit of radioactivity defined in 1910. It was originally defined as equivalent to the number of disintegrations that one gram of radium-226 will undergo in one second. Currently, a curie is defined as 1Ci = 3.7 x 1010 disintegrations per second.
- Rutherford. Rutherford (symbol Rd) is also a non-SI unit defined as the activity of a quantity of radioactive material in which one million nuclei decay per second.
See also: Radiation Dosimetry
Radioactive Decay Law
Calculations of the decay of radioactive nuclei are relatively straightforward because there is only one fundamental law governing all decay processes. This law states that the probability per unit time that a nucleus will decay is constant, independent of time. This constant is called the decay constant and is denoted by λ, “lambda”. The radioactive decay of a certain number of atoms (mass) is exponential in time.
Radioactive decay law: N = N.e-λt
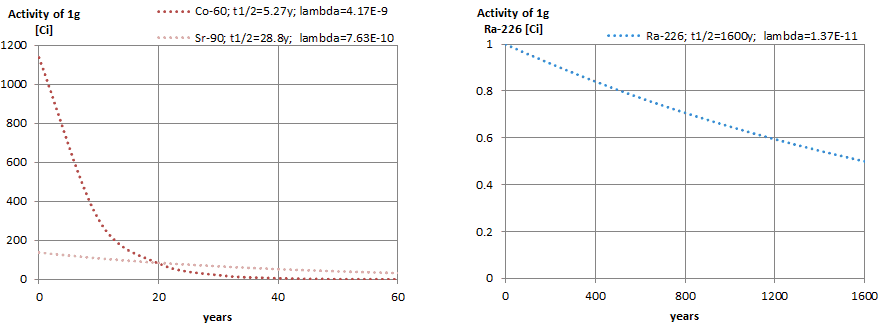
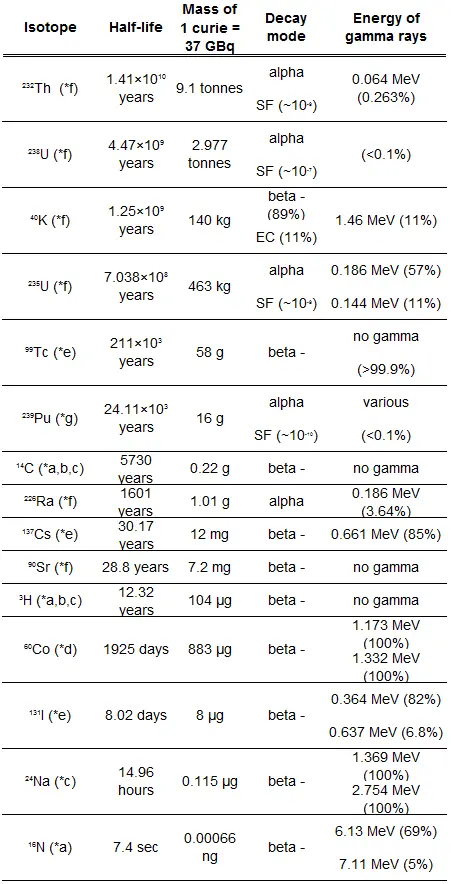
The rate of nuclear decay is also measured in terms of half-lives. The half-life is the amount of time it takes for a given isotope to lose half of its radioactivity. If a radioisotope has a half-life of 14 days, half of its atoms will have decayed within 14 days. In 14 more days, half of that remaining half will decay, and so on. Half-lives range from millionths of a second for highly radioactive fission products to billions of years for long-lived materials (such as naturally occurring uranium). Notice that short half-lives go with large decay constants. Radioactive material with a short half-life is much more radioactive (at the time of production) but will obviously lose its radioactivity rapidly. No matter how long or short, the half-life is after seven half-lives have passed, less than 1 percent of the initial activity remaining.
The radioactive decay law can also be derived for activity calculations or mass of radioactive material calculations:
(Number of nuclei) N = N.e-λt (Activity) A = A.e-λt (Mass) m = m.e-λt
Where N (number of particles) is the total number of particles in the sample, A (total activity) is the number of decays per unit time of a radioactive sample, m is the mass of remaining radioactive material.
Half-Life and Decay Constant
In radioactivity calculations, one of two parameters (decay constant or half-life), which characterize the rate of decay, must be known. There is a relation between the half-life (t1/2) and the decay constant λ. The relationship can be derived from decay law by setting N = ½ No. This gives:
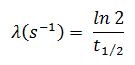where ln 2 (the natural log of 2) equals 0.693. If the decay constant (λ) is given, it is easy to calculate the half-life, and vice-versa.
Half-Life and Radioactivity – Example
The relationship between half-life and the amount of a radionuclide required to give an activity of one curie is shown in the figure. This amount of material can be calculated using λ, which is the decay constant of certain nuclide:
The following figure illustrates the amount of material necessary for 1 curie of radioactivity. Obviously, the longer the half-life, the greater the quantity of radionuclide needed to produce the same activity. Of course, the longer-lived substance will remain radioactive for a much longer time. As can be seen, the amount of material necessary for 1 curie of radioactivity can vary from an amount too small to be seen (0.00088 gram of cobalt-60), through 1 gram of radium-226, to almost three tons of uranium-238.
Example – Radioactive Decay Law
A sample of material contains 1 microgram of iodine-131. Note that iodine-131 plays a major role as a radioactive isotope present in nuclear fission products and contributes to health hazards when released into the atmosphere during an accident. Iodine-131 has a half-life of 8.02 days.
Calculate:
- The number of iodine-131 atoms is initially present.
- The activity of the iodine-131 in curies.
- The number of iodine-131 atoms will remain in 50 days.
- The time it will take for the activity to reach 0.1 mCi.
Solution:
- The number of atoms of iodine-131 can be determined using isotopic mass as below.
NI-131 = mI-131 . NA / MI-131
NI-131 = (1 μg) x (6.02×1023 nuclei/mol) / (130.91 g/mol)
NI-131 = 4.6 x 1015 nuclei
- The activity of the iodine-131 in curies can be determined using its decay constant:
In radioactivity calculations, one of two parameters (decay constant or half-life), which characterize the rate of decay, must be known. There is a relation between the half-life (t1/2) and the decay constant λ. The relationship can be derived from decay law by setting N = ½ No. This gives:
where ln 2 (the natural log of 2) equals 0.693. If the decay constant (λ) is given, it is easy to calculate the half-life, and vice-versa.
The iodine-131 has a half-life of 8.02 days (692928 sec), and therefore its decay constant is:
Using this value for the decay constant, we can determine the activity of the sample:
3) and 4) The number of iodine-131 atoms that will remain in 50 days (N50d) and the time it will take for the activity to reach 0.1 mCi can be calculated using the decay law:
As can be seen, after 50 days, the number of iodine-131 atoms and thus the activity will be about 75 times lower. After 82 days, the activity will be approximately 1200 times lower. Therefore, the time of ten half-lives (factor 210 = 1024) is widely used to define residual activity.
Decay Chain
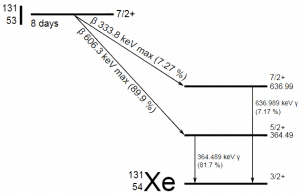
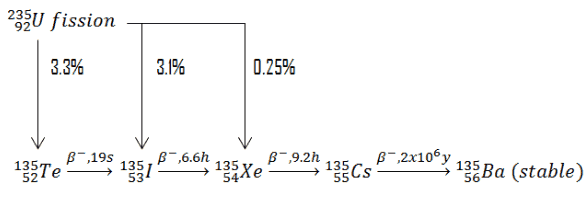In physics, a radioactive decay chain is a sequence of unstable atomic nuclei and their modes of decays, which leads to a stable nucleus. Sources of these unstable nuclei are different, but engineers mostly deal with naturally occurring radioactive decay chains known as radioactive series. Note that, in nuclear reactors, there are many types of decay chains of fission fragments. Fission fragments are highly unstable (radioactive) and undergo further radioactive decays to stabilize themselves.
See also: Radioactive Decay Chain
Decay Heat in Reactor
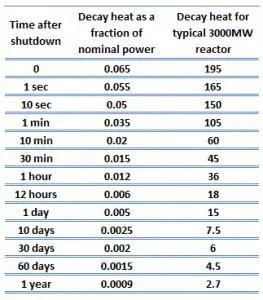
When a reactor is shut down, fission essentially ceases, but decay energy is still being produced. The energy produced after shutdown is referred to as decay heat. The amount of decay heat production after shutdown is directly influenced by the reactor’s power history (fission products accumulation) prior to shutdown and by the level of fuel burnup (actinides accumulation – especially in case of spent fuel handling). A reactor operated at full power for 10 days prior to the shutdown has much higher decay heat generation than a reactor operated at low power for the same period. On the other hand, when the reactor changes its power from 50% to 100% of full power, the ratio of decay heat to neutron power drops to roughly half its previous level. It then builds up slowly as the fission product inventory adjusts to the new power.
The decay heat produced after a reactor shutdown from full power is initially equivalent to about 6 to 7% of the rated thermal power. Since radioactive decay is a random process at the level of single atoms, it is governed by the radioactive decay law. Note that irradiated nuclear fuel contains a large number of different isotopes that contribute to decay heat, which is all subject to the radioactive decay law. Therefore a model describing decay heat must consider decay heat to be a sum of exponential functions with different decay constants and initial contribution to the heat rate. Fission fragments with a short half-life are much more radioactive (at the time of production) and contribute significantly to decay heat but will obviously lose their share rapidly. On the other hand, fission fragments and transuranic elements with a long half-life are less radioactive (at the time of production) and produce less decay heat but will obviously lose their share more slowly. This decay heat generation rate diminishes to about 1% approximately one hour after shutdown.