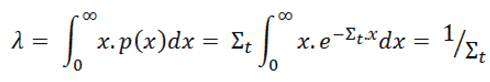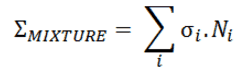At this point we have to distinguish between two basic types of nuclear or neutron cross-sections.
- Microscopic Cross-section. The effective target area in m2 presented by a single nucleus to an incident neutron beam is denoted the microscopic cross section, σ. The microscopic cross-sections characterize interactions with single isotopes and are a part of data libraries, such as ENDF/B-VII.1.
- Macroscopic Cross-section. The macroscopic cross-section represents the effective target area of all of the nuclei contained in the volume of the material (such as fuel pellet). The units are given in cm-1. It is the probability of neutron-nucleus interaction per centimeter of neutron travel. These data are commonly used by codes for reactor core analyses and design. These codes are based on pre-computed assembly homogenized macroscopic cross-sections.

Barn – Unit of Cross-section
The cross-section is typically denoted σ and measured in units of area [m2]. But a square meter (or centimeter) is tremendously large in comparison to the effective area of a nucleus, and it has been suggested that a physicist once referred to the measure of a square meter as being “as big as a barn” when applied to nuclear processes. The name has persisted and microscopic cross sections are expressed in terms of barns. The standard unit for measuring a nuclear cross section is the barn, which is equal to 10−28 m² or 10−24 cm². It can be seen the concept of a nuclear cross section can be quantified physically in terms of “characteristic target area” where a larger area means a larger probability of interaction.
Typical Values of Microscopic Cross-sections
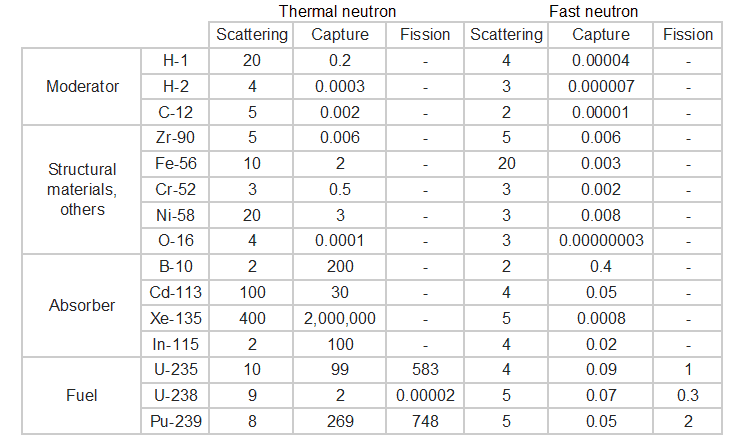
- Uranium 235 is a fissile isotope and its fission cross-section for thermal neutrons is about 585 barns (for 0.0253 eV neutron). For fast neutrons its fission cross-section is on the order of barns.
- Xenon-135 is a product of U-235 fission and has a very large neutron capture cross-section (about 2.6 x 106 barns).
- Boron is commonly used as a neutron absorber due to the high neutron cross-section of isotope 10B. Its (n,alpha) reaction cross-section for thermal neutrons is about 3840 barns (for 0.025 eV neutron).
- Gadolinium is commonly used as a neutron absorber due to very high neutron absorbtion cross-section of two isotopes 155Gd and 157Gd. 155Gd has 61 000 barns for thermal neutrons (for 0.025 eV neutron) and 157Gd has even 254 000 barns.
See also: JANIS (Java-based Nuclear Data Information Software)
Microscopic Cross-section
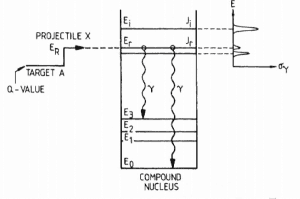
The extent to which neutrons interact with nuclei is described in terms of quantities known as cross-sections. Cross-sections are used to express the likelihood of particular interaction between an incident neutron and a target nucleus. It must be noted this likelihood does not depend on real target dimensions. In conjunction with the neutron flux, it enables the calculation of the reaction rate, for example to derive the thermal power of a nuclear power plant. The standard unit for measuring the microscopic cross-section (σ-sigma) is the barn, which is equal to 10-28 m2. This unit is very small, therefore barns (abbreviated as “b”) are commonly used.
The cross-section σ can be interpreted as the effective ‘target area’ that a nucleus interacts with an incident neutron. The larger the effective area, the greater the probability for reaction. This cross-section is usually known as the microscopic cross-section.
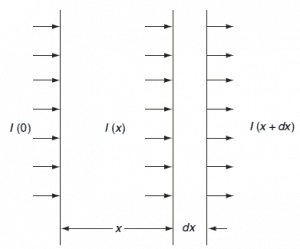
The concept of the microscopic cross-section is therefore introduced to represent the probability of a neutron-nucleus reaction. Suppose that a thin ‘film’ of atoms (one atomic layer thick) with Na atoms/cm2 is placed in a monodirectional beam of intensity I0. Then the number of interactions C per cm2 per second will be proportional to the intensity I0 and the atom density Na. We define the proportionality factor as the microscopic cross-section σ:
σt = C/Na.I0
In order to be able to determine the microscopic cross section, transmission measurements are performed on plates of materials. Assume that if a neutron collides with a nucleus it will either be scattered into a different direction or be absorbed (without fission absorption). Assume that there are N (nuclei/cm3) of the material and there will then be N.dx per cm2 in the layer dx.
Only the neutrons that have not interacted will remain traveling in the x direction. This causes the intensity of the uncollided beam will be attenuated as it penetrates deeper into the material.
Then, according to the definition of the microscopic cross section, the reaction rate per unit area is Nσ Ι(x)dx. This is equal to the decrease of the beam intensity, so that:
-dI = N.σ.Ι(x).dx
and
Ι(x) = Ι0e-N.σ.x
It can be seen that whether a neutron will interact with a certain volume of material depends not only on the microscopic cross-section of the individual nuclei but also on the density of nuclei within that volume. It depends on the N.σ factor. This factor is therefore widely defined and it is known as the macroscopic cross section.
The difference between the microscopic and macroscopic cross sections is extremely important. The microscopic cross section represents the effective target area of a single nucleus, while the macroscopic cross section represents the effective target area of all of the nuclei contained in certain volume.
Microscopic cross-sections constitute a key parameters of nuclear fuel. In general, neutron cross-sections are essential for the reactor core calculations and are a part of data libraries, such as ENDF/B-VII.1.
The neutron cross-section is variable and depends on:
 Target nucleus (hydrogen, boron, uranium, etc.). Each isotop has its own set of cross-sections.
Target nucleus (hydrogen, boron, uranium, etc.). Each isotop has its own set of cross-sections.- Type of the reaction (capture, fission, etc.). Cross-sections are different for each nuclear reaction.
- Neutron energy (thermal neutron, resonance neutron, fast neutron). For a given target and reaction type, the cross-section is strongly dependent on the neutron energy. In the common case, the cross section is usually much larger at low energies than at high energies. This is why most nuclear reactors use a neutron moderator to reduce the energy of the neutron and thus increase the probability of fission, essential to produce energy and sustain the chain reaction.
- Target energy (temperature of target material – Doppler broadening). This dependency is not so significant, but the target energy strongly influences inherent safety of nuclear reactors due to a Doppler broadening of resonances.
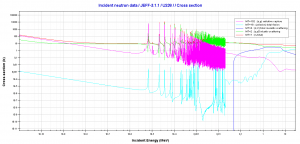
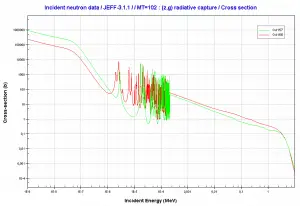
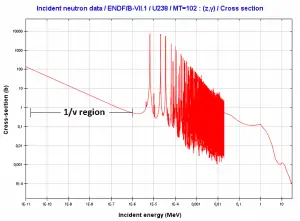
Microscopic cross-section varies with incident neutron energy. Some nuclear reactions exhibit very specific dependency on incident neutron energy. This dependency will be described on the example of the radiative capture reaction. The likelihood of a neutron radiative capture is represented by the radiative capture cross section as σγ. The following dependency is typical for radiative capture, it definitely does not mean, that it is typical for other types of reactions (see elastic scattering cross-section or (n,alpha) reaction cross-section).
The capture cross-section can be divided into three regions according to the incident neutron energy. These regions will be discussed separately.
- 1/v Region
- Resonance Region
- Fast Neutrons Region
Macroscopic Cross-section
The difference between the microscopic cross-section and macroscopic cross-section is very important and is restated for clarity. The microscopic cross section represents the effective target area of a single target nucleus for an incident particle. The units are given in barns or cm2.
While the macroscopic cross-section represents the effective target area of all of the nuclei contained in the volume of the material. The units are given in cm-1.
A macroscopic cross-section is derived from microscopic cross-section and the atomic number density:
Σ=σ.N
Here σ, which has units of m2, is the microscopic cross-section. Since the units of N (nuclei density) are nuclei/m3, the macroscopic cross-section Σ have units of m-1, thus in fact is an incorrect name, because it is not a correct unit of cross-sections. In terms of Σt (the total cross-section), the equation for the intensity of a neutron beam can be written as
-dI = N.σ.Σt.dx
Dividing this expression by I(x) gives
-dΙ(x)/I(x) = Σt.dx
Since dI(x) is the number of neutrons that collide in dx, the quantity –dΙ(x)/I(x) represents the probability that a neutron that has survived without colliding until x, will collide in the next layer dx. It follows that the probability P(x) that a neutron will travel a distance x without any interaction in the material, which is characterized by Σt, is:
P(x) = e-Σt.x
From this equation, we can derive the probability that a neutron will make its first collision in dx. It will be the quantity P(x)dx. If the probability of the first collision in dx is independent of its past history, the required result will be equal to the probability that a neutron survives up to layer x without any interaction (~Σtdx) times the probability that the neutron will interact in the additional layer dx (i.e., ~e-Σt.x).
P(x)dx = Σtdx . e-Σt.x = Σt e-Σt.x dx
Mean Free Path
From the equation for the probability of the first collision in dx we can calculate the mean free path that is traveled by a neutron between two collisions. This quantity is usually designated by the symbol λ and it is equal to the average value of x, the distance traveled by a neutron without any interaction, over the interaction probability distribution.
whereby one can distinguish λs, λa, λf, etc. This quantity is also known as the relaxation length, because it is the distance in which the intensity of the neutrons that have not caused a reaction has decreased with a factor e.
For materials with high absorption cross-section, the mean free path is very short and neutron absorption occurs mostly on the surface of the material. This surface absorption is called self-shielding because the outer layers of atoms shield the inner layers.
Macroscopic Cross-section of Mixtures and Molecules
Most materials are composed of several chemical elements and compounds. Most of chemical elements contains several isotopes of these elements (e.g., gadolinium with its six stable isotopes). For this reason most materials involve many cross-sections. Therefore, to include all the isotopes within a given material, it is necessary to determine the macroscopic cross section for each isotope and then sum all the individual macroscopic cross-sections.
In this section both factors (different atomic densities and different cross-sections) will be considered in the calculation of the macroscopic cross-section of mixtures.
First, consider the Avogadro’s number N0 = 6.022 x 1023, is the number of particles (molecules, atoms) that is contained in the amount of substance given by one mole. Thus if M is the molecular weight, the ratio N0/M equals to the number of molecules in 1g of the mixture. The number of molecules per cm3 in the material of density ρ and the macroscopic cross-section for mixtures are given by following equations:
Ni = ρi.N0 / Mi
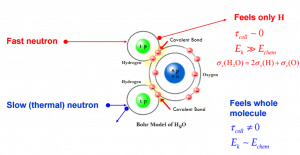
Note that, in some cases, the cross-section of the molecule is not equal to the sum of cross-sections of its individual nuclei. For example the cross-section of neutron elastic scattering of water exhibits anomalies for thermal neutrons. It occurs, because the kinetic energy of an incident neutron is of the order or less than the chemical binding energy and therefore the scattering of slow neutrons by water (H2O) is greater than by free nuclei (2H + O).
Doppler Broadening of Resonances
In general, Doppler broadening is the broadening of spectral lines due to the Doppler effect caused by a distribution of kinetic energies of molecules or atoms. In reactor physics a particular case of this phenomenon is the thermal Doppler broadening of the resonance capture cross sections of the fertile material (e.g., 238U or 240Pu) caused by thermal motion of target nuclei in the nuclear fuel.
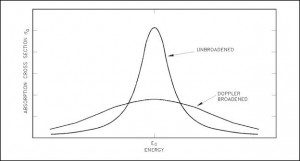
The Doppler broadening of resonances is very important phenomenon, which improves reactor stability, because it accounts for the dominant part of the fuel temperature coefficient (the change in reactivity per degree change in fuel temperature) in thermal reactors and makes a substantial contribution in fast reactors as well. This coefficient is also called the prompt temperature coefficient because it causes an immediate response on changes in fuel temperature. The prompt temperature coefficient of most thermal reactors is negative.
See also: Doppler Broadening
Self-Shielding
It was written, in some cases the amount of absorption reactions is dramatically reduced despite the unchanged microscopic cross-section of the material. This phenomena is commonly known as the resonance self-shielding and also contributes to to the reactor stability. There are two types of self-shielding.
- Energy Self-shielding.
- Spatial Self-shielding.
See also: Resonance Self-shielding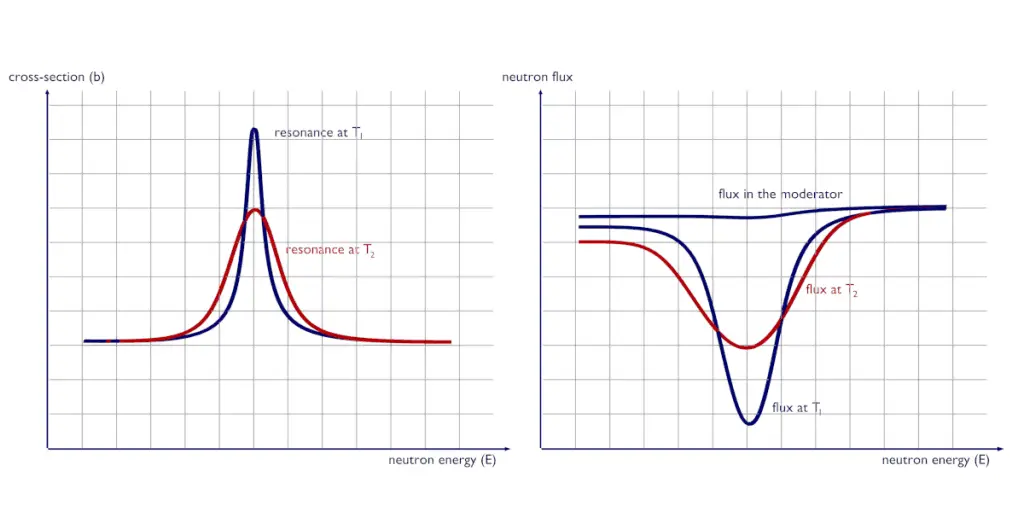 An increase in temperature from T1 to T2 causes the broadening of spectral lines of resonances. Although the area under the resonance remains the same, the broadening of spectral lines causes an increase in neutron flux in the fuel φf(E), which in turn increases the absorption as the temperature increases.
An increase in temperature from T1 to T2 causes the broadening of spectral lines of resonances. Although the area under the resonance remains the same, the broadening of spectral lines causes an increase in neutron flux in the fuel φf(E), which in turn increases the absorption as the temperature increases.