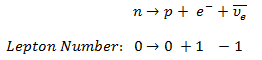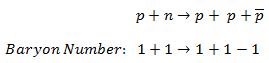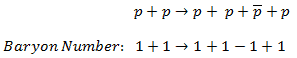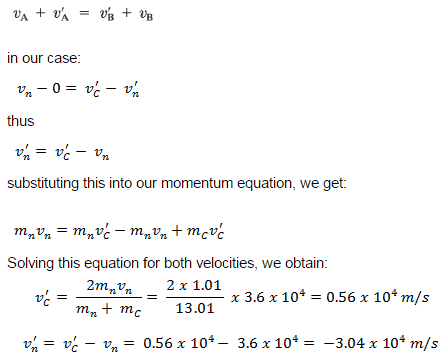Article Summary & FAQs
What is a nuclear reaction?
A nuclear reaction is considered to be the process in which two atomic nuclei or subatomic particles interact to produce one or more new particles or gamma rays.
Key Facts
- Perhaps the most notable nuclear reactions are the nuclear fusion reactions of light elements that power the energy production of stars and the Sun.
- The most notable man-controlled nuclear reaction is the fission reaction which occurs in nuclear reactors.
- Classification of nuclear reactions is according to the time scale of these reactions.
- In direct nuclear reactions, a projectile and a target nucleus are within the range of nuclear forces for a very short time allowing for an interaction of a single nucleon only.
- In compound nuclear reactions, a projectile and a target nucleus are within the range of nuclear forces for the time allowing for a large number of interactions between nucleons.
- 10B(n,alpha)7Li is typical notation of nuclear reactions.
- Energetics of nuclear reactions is determined by the Q-value of that reaction.
A nuclear reaction is a process when two atomic nuclei or subatomic particles interact to produce one or more new particles or gamma rays. Thus, a nuclear reaction must cause a transformation of at least one nuclide to another. Sometimes if a nucleus interacts with another nucleus or particle without changing the nature of any nuclide, the process is referred to as a nuclear scattering rather than a nuclear reaction. Perhaps the most notable nuclear reactions are the nuclear fusion reactions of light elements that power the energy production of stars and the Sun. Natural nuclear reactions also occur in the interaction between cosmic rays and matter.
The most notable man-controlled nuclear reaction is the fission reaction which occurs in nuclear reactors. Nuclear reactors are devices to initiate and control a nuclear chain reaction, but there are not only artificial devices. The world’s first nuclear reactor operated about two billion years ago. The natural nuclear reactor formed at Oklo in Gabon, Africa, when a uranium-rich mineral deposit became flooded with groundwater that acted as a neutron moderator, and a nuclear chain reaction started. These fission reactions were sustained for hundreds of thousands of years until a chain reaction could be supported no longer. This was confirmed by the existence of isotopes of the fission-product gas xenon and by different ratios of U-235/U-238 (enrichment of natural uranium).
See also: JANIS – Java-based Nuclear Data Information System
See also: Neutron Reactions
Notation of Nuclear Reactions
Standard nuclear notation shows (see picture) the chemical symbol, the mass number, and the atomic number of the isotope.
If the initial nuclei are denoted by a and b, and the product nuclei are denoted by c and d, the reaction can be represented by the equation:
a + b → c + d
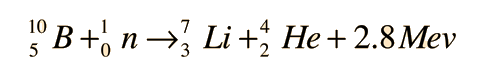
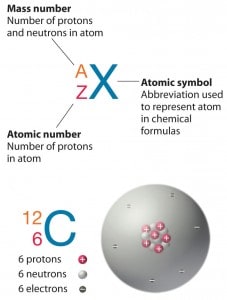
Source: chemwiki.ucdavis.edu
Instead of using the full equations in the style above, a compact notation describes nuclear reactions in many situations. This style of the form a(b,c)d is equivalent to a + b producing c + d. Light particles are often abbreviated in this shorthand, typically p means proton, n means neutron, d means deuteron, α means an alpha particle or helium-4, β means beta particle or electron, γ means gamma photon, etc. The reaction above would be written as 10B(n,α)7Li.
Basic Classification of Nuclear Reactions
To understand the nature of neutron nuclear reactions, the classification according to the time scale of these reactions has to be introduced. Interaction time is critical for defining the reaction mechanism.
There are two extreme scenarios for nuclear reactions (not only neutron reactions):
- A projectile and a target nucleus are within the range of nuclear forces for a very short time allowing for an interaction of a single nucleon only. These types of reactions are called direct reactions.
- A projectile and a target nucleus are within the range of nuclear forces, allowing for many interactions between nucleons. These types of reactions are called the compound nucleus reactions.
In fact, there is always some non-direct (multiple internuclear interaction) component in all reactions, but the direct reactions have this component limited.
Types of Nuclear Reactions
Although the number of possible nuclear reactions is enormous, nuclear reactions can be sorted by type. Most nuclear reactions are accompanied by gamma emissions. Some examples are:
- Elastic scattering. In elastic scattering, the kinetic energy of a particle is conserved in the center-of-mass frame, but its direction of propagation is modified. There is no energy transferred into nuclear excitation in an elastic scattering reaction. It is a crucial reaction for neutron moderators in nuclear reactors. To be an effective moderator, the probability of an elastic reaction between the neutron and the nucleus must be high.
1H (n, n) 1H
- Inelastic scattering. In inelastic scattering, the particle is absorbed and then re-emitted. The difference of kinetic energies is saved in an excited nuclide. An inelastic scattering plays an important role in slowing down neutrons, especially at high energies and by heavy nuclei.
238U (n, n’) 238U*
- Capture reaction. The capture reaction is one of the two possible absorption reactions that may occur. Capture reactions result in the loss of a neutron coupled with the production of one or more gamma rays. The resulting nucleus may also undergo a subsequent decay, such as beta decay in this example, which is a very important reaction in nuclear fuel.
238U (n, ˠ) 239U
- Transfer Reaction. Transfer reactions are nuclear reactions in which one or more nucleons are transferred to the other nucleus. Transfer reactions can occur from the projectile to the target; stripping reactions, or from the target to the projectile; pick-up reactions. These reactions are common in particle accelerators and astrophysics.
4He (α, p) 7Li
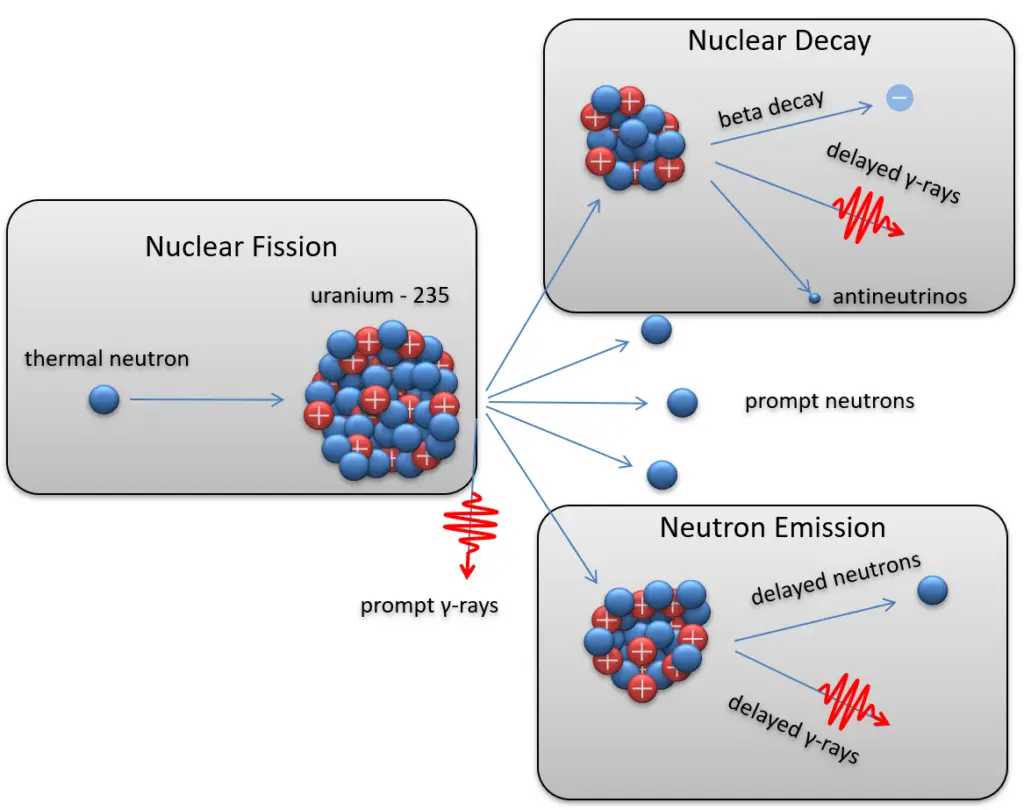
- Fission reactions. Nuclear fission is a nuclear reaction in which the nucleus of an atom splits into smaller parts (lighter nuclei). The fission process often produces free neutrons and photons (in the form of gamma rays) and releases a large amount of energy.
235U (n, 3n) fission products
- Fusion reactions. Occur when two or more atomic nuclei collide at a very high speed and join to form a new type of atomic nucleus. The fusion reaction of deuterium and tritium is exciting because of its potential of providing energy for the future.
3T (d, n) 4He
- Spallation reactions. Spallation reaction occurs when a particle hits a nucleus with sufficient energy and momentum to knock out several small fragments or smash them into many fragments. Nuclear spallation is one of the processes by which a particle accelerator may be used to produce a beam of neutrons.
209Bi (α,xn)213-xAt
- Nuclear decay (Radioactive decay). Occurs when an unstable atom loses energy by emitting ionizing radiation. Radioactive decay is a random process at the level of single atoms, in that, according to quantum theory, it is impossible to predict when a particular atom will decay. There are many types of radioactive decay:
- Alpha radioactivity. Alpha particles consist of two protons and two neutrons bound together into a particle identical to a helium nucleus. Because of its huge mass (more than 7000 times the mass of the beta particle) and its charge, it heavily ionizes material and has a very short range.
-
- Beta radioactivity. Beta particles are high-energy, high-speed electrons or positrons emitted by specific radioactive nuclei such as potassium-40. The beta particles emitted are a form of ionizing radiation, also known as beta rays. The beta particles have a greater range of penetration than alpha particles but still much less than gamma rays. The production of beta particles is termed beta decay.
-
- Gamma radioactivity. Gamma rays are electromagnetic radiation of a very high frequency and are therefore high-energy photons. Nuclei decay produces them as they transition from a high-energy state to a lower state known as gamma decay. Most nuclear reactions are accompanied by gamma emissions.
-
- Neutron emission. Neutron emission is a type of radioactive decay of nuclei containing excess neutrons (especially fission products), in which a neutron is simply ejected from the nucleus. This type of radiation plays a key role in nuclear reactor control because these neutrons are delayed neutrons.
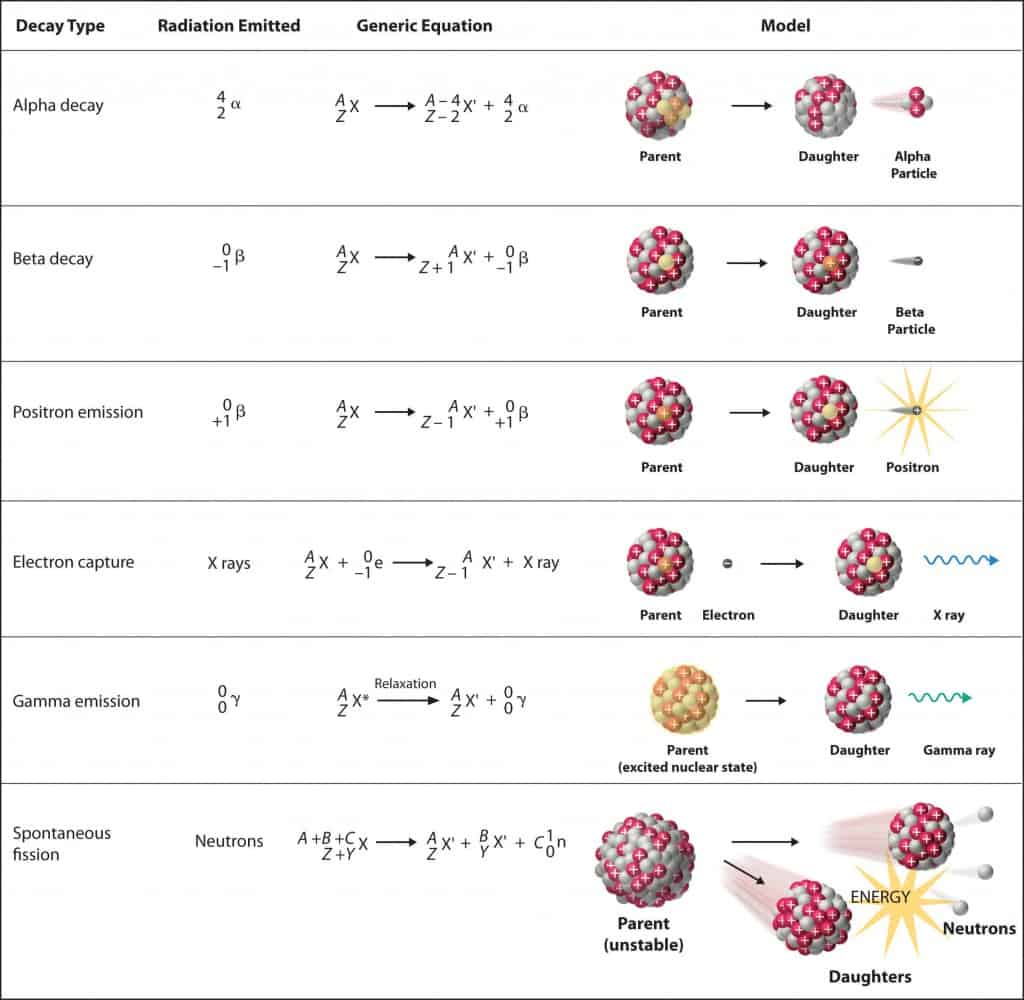
Source: chemwiki.ucdavis.edu
Main Characteristics of Nuclear Reactions
In nuclear physics, the nuclear cross-section of a nucleus is commonly used to characterize the probability that a nuclear reaction will occur. The cross-section is typically denoted σ and measured in units of the area [m2]. The standard unit for measuring a nuclear cross-section is the barn, equal to 10−28 m² or 10−24 cm². It can be seen that the concept of a nuclear cross-section can be quantified physically using a “characteristic target area,” where a larger area means a larger probability of interaction.
 For a given event, the cross-section σ is given by
For a given event, the cross-section σ is given by
σ = μ/n
where
- σ is the cross-section of this event [m2],
- μ is the attenuation coefficient due to the occurrence of this event [m-1],
- n is the density of the target particles [m-3].
Conservation Laws in Nuclear Reactions
In analyzing nuclear reactions, we apply the many conservation laws. Nuclear reactions are subject to classical conservation laws for the charge, momentum, angular momentum, and energy(including rest energies). Other conservation laws, not anticipated by classical physics, are:
- Law of Conservation of Lepton Number
- Law of Conservation of Baryon Number
- Law of Conservation of Electric Charge
Certain of these laws are obeyed under all circumstances, and others are not. We have accepted the conservation of energy and momentum. In all the examples given, we assume that the number of protons and the number of neutrons is separately conserved. We shall find circumstances and conditions in which this rule is not true. Where we are considering non-relativistic nuclear reactions, it is essentially true. However, we shall find that these principles must be extended when we consider relativistic nuclear energies or those involving weak interactions.
Some conservation principles have arisen from theoretical considerations, and others are just empirical relationships. Notwithstanding, any reaction not expressly forbidden by the conservation laws will generally occur, if perhaps at a slow rate. This expectation is based on quantum mechanics. Unless the barrier between the initial and final states is infinitely high, there is always a non-zero probability that a system will make the transition between them.
The non-relativistic reactions are governing by four of the fundamental laws and to analyze them is necessary to follow them:
- Conservation of nucleons. The total number of nucleons before and after a reaction are the same.
- Conservation of charge. The sum of the charges on all the particles before and after a reaction are the same.
- Conservation of momentum. The total momentum of the interacting particles before and after a reaction is the same.
- Conservation of energy. Energy, including rest mass energy, is conserved in nuclear reactions.
Reference: Lamarsh, John R. Introduction to Nuclear engineering 2nd Edition.
Elastic Nuclear Collision
A neutron (n) of mass 1.01 u traveling with a speed of 3.60 x 104m/s interacts with a carbon (C) nucleus (mC = 12.00 u) initially at rest in an elastic head-on collision.
What are the velocities of the neutron and carbon nucleus after the collision?
Solution:
This is an elastic head-on collision of two objects with unequal masses. We have to use the conservation laws of momentum and kinetic energy and apply them to our system of two particles.
We can solve this equation system, or we can use the equation derived in the previous section. This equation stated that the relative speed of the two objects after the collision has the same magnitude (but opposite direction) as before the collision, no matter what the masses are.
The minus sign for v’ tells us that the neutron scatters the back of the carbon nucleus because the carbon nucleus is significantly heavier. On the other hand, its speed is less than its initial speed. This process is known as neutron moderation, and it significantly depends on the mass of moderator nuclei.
Energetics of Nuclear Reactions – Q-value
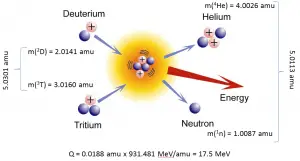
In nuclear and particle physics, the energetics of nuclear reactions are determined by the reaction’s Q-value. The Q-value of the reaction is defined as the difference between the sum of the masses of the initial reactants and the sum of the masses of the final products in energy units (usually in MeV).
Consider a typical reaction in which the projectile a and target A place to two products, B and b. This can also be expressed in the notation we have used so far, a + A → B + b, or even in a more compact notation, A(a,b)B.
See also: E=mc2
The Q-value of this reaction is given by:
Q = [ma + mA – (mb + mB)]c2
which is the same as the excess kinetic energy of the final products:
Q = Tfinal – Tinitial
= Tb + TB – (Ta + TA)
For reactions in which there is an increase in the kinetic energy of the products, Q is positive. The positive Q reactions are said to be exothermic (or exergic). There is a net release of energy since the kinetic energy of the final state is greater than the kinetic energy of the initial state.
For reactions in which there is a decrease in the kinetic energy of the product, Q is negative. The negative Q reactions are endothermic (or endoergic), and they require net energy input.
The energy released in a nuclear reaction can appear mainly in one of three ways:
- The kinetic energy of the products.
- Emission of gamma rays. Gamma rays are emitted by unstable nuclei in their transition from a high-energy state to a lower state known as gamma decay.
- Metastable state. Some energy may remain in the nucleus as a metastable energy level.
A small amount of energy may also emerge in the form of X-rays. Generally, products of nuclear reactions may have different atomic numbers, and thus the configuration of their electron shells is different in comparison with reactants. As the electrons rearrange themselves and drop to lower energy levels, internal transition X-rays (X-rays with precisely defined emission lines) may be emitted.
Exothermic Reactions
Endothermic Reactions
Test your Knowledge – Nuclear Reactions
With our simple quizzes, you can test your knowledge.
It is intuitive: start quiz and answer questions.